EVALUATING LIMITS FROM A GRAPH WORKSHEET

Evaluate the following using the graph shown below.

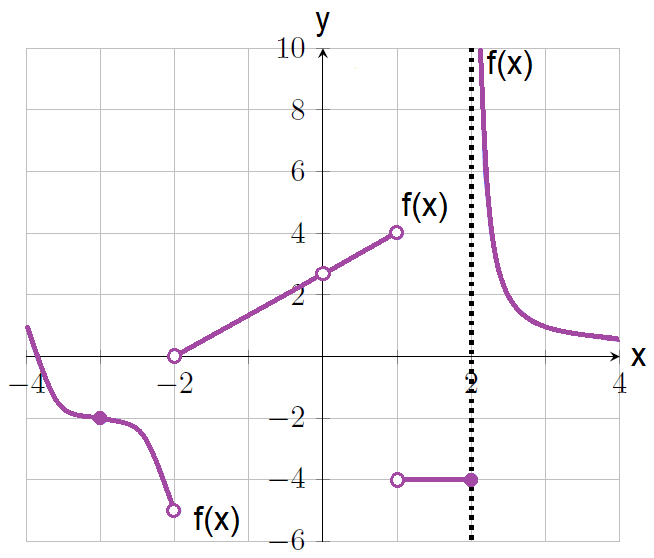
Problem 1 :

                                       lim    f(x)
                                    x--> -3^-

Problem 2 :

                                       lim     f(x)
                                    x--> -3⁺

Problem 3 :

                                       lim     f(x)
                                    x--> -3

Problem 4 :

                                       lim    f(x)
                                    x--> -2^-

Problem 5 :

                                       lim     f(x)
                                    x--> -2⁺

Problem 6 :

                                       lim     f(x)
                                    x--> -2

Problem 7 :

                                       lim    f(x)
                                    x--> 0^-

Problem 8 :

                                       lim     f(x)
                                    x--> 0⁺

Problem 9 :

                                       lim     f(x)
                                    x--> 0

Problem 10 :

                                       lim    f(x)
                                    x--> 1^-

Problem 11 :

                                       lim     f(x)
                                    x--> 1⁺

Problem 12 :

                                       lim     f(x)
                                    x--> 1

Problem 13 :

                                       lim    f(x)
                                    x--> 2^-

Problem 14 :

                                       lim     f(x)
                                    x--> 2⁺

Problem 15 :

                                       lim     f(x)
                                    x--> 2

Answers

1. Answer :

                                       lim    f(x)
                                    x--> -3^-

We have to evaluate left-sided limit of f(x) as x tends to -3.

In the graph shown above, when x tends to -3 from its left side, f(x) tends to -2.

Therefore,

                                       lim     f(x) = -2
                                    x--> -3^-

2. Answer :

                                       lim     f(x)
                                    x--> -3⁺

We have to evaluate right-sided limit of f(x) as x tends to -3.

In the graph shown above, when x tends to -3 from its right side, f(x) tends to -2.

Therefore,

                                       lim     f(x) = -2
                                    x--> -3⁺

3. Answer :

                                       lim     f(x)
                                    x--> -3

We have to evaluate two-sided limit of f(x) as x tends to -3.

From the answers (1 and 2) above, we have

                           lim     f(x)   =   lim     f(x)
                           x--> -3^-              x--> -3⁺

Since, the left-sided limit and right sided limit are equal, two-sided limit exists.

That is,

                                       lim     f(x) = -2
                                    x--> -3

4. Answer :

                                       lim    f(x)
                                    x--> -2^-

We have to evaluate left-sided limit of f(x) as x tends to -2.

In the graph shown above, when x tends to -2 from its left side, f(x) tends to -5.

Therefore,

                                       lim     f(x) = -5
                                    x--> -2^-

5. Answer :

                                       lim     f(x)
                                    x--> -2⁺

We have to evaluate right-sided limit of f(x) as x tends to -2.

In the graph shown above, when x tends to -2 from its right side, f(x) tends to 0.

Therefore,

                                       lim     f(x) = 0
                                    x--> -2⁺

6. Answer :

                                       lim     f(x)
                                    x--> -2

We have to evaluate two-sided limit of f(x) as x tends to -2.

From the answers (4 and 5) above, we have

                           lim     f(x)   ≠   lim     f(x)
                           x--> -2^-              x--> -2⁺

Since, the left-sided limit and right sided limit are not equal, two-sided limit does not exist.

That is,

                           lim     f(x) does not exist
                        x--> -2

7. Answer :

                                       lim    f(x)
                                    x--> 0^-

We have to evaluate left-sided limit of f(x) as x tends to 0.

In the graph shown above, when x tends to 0 from its left side, f(x) tends to 2.7.

Therefore,

                                       lim     f(x) = 2.7
                                    x--> -0^-

8. Answer :

                                       lim     f(x)
                                    x--> 0⁺

We have to evaluate right-sided limit of f(x) as x tends to 0.

In the graph shown above, when x tends to 0 from its right side, f(x) tends to 2.7.

Therefore,

                                       lim     f(x) = 2.7
                                    x--> 0⁺

9. Answer :

                                       lim     f(x)
                                    x--> 0

We have to evaluate two-sided limit of f(x) as x tends to 0.

From the answers (7 and 8) above, we have

                           lim     f(x)   =   lim     f(x)
                           x--> 0^-              x--> 0⁺

Since, the left-sided limit and right sided limit are equal, two-sided limit exists.

That is,

                                       lim     f(x) = 2.7
                                    x--> 0

10. Answer :

                                       lim    f(x)
                                    x--> 1^-

We have to evaluate left-sided limit of f(x) as x tends to 1.

In the graph shown above, when x tends to 1 from its left side, f(x) tends to 4.

Therefore,

                                       lim     f(x) = 4
                                    x--> 1^-

11. Answer :

                                       lim     f(x)
                                    x--> 1⁺

We have to evaluate right-sided limit of f(x) as x tends to 1.

In the graph shown above, when x tends to 1 from its right side, f(x) tends to -4.

Therefore,

                                       lim     f(x) = -4
                                    x--> 1⁺

12. Answer :

                                       lim     f(x)
                                    x--> 1

We have to evaluate two-sided limit of f(x) as x tends to 1.

From the answers (10 and 11) above, we have

                           lim     f(x)   ≠   lim     f(x)
                           x--> 1^-              x--> 1⁺

Since, the left-sided limit and right sided limit are not equal, two-sided limit does not exist.

That is,

                           lim     f(x) does not exist
                        x--> 1

13. Answer :

                                       lim    f(x)
                                    x--> 2^-

We have to evaluate left-sided limit of f(x) as x tends to 2.

In the graph shown above, when x tends to 2 from its left side, f(x) tends to -4.

Therefore,

                                       lim     f(x) = -4
                                    x--> 2^-

14. Answer :

                                       lim     f(x)
                                    x--> 2⁺

We have to evaluate right-sided limit of f(x) as x tends to 2.

In the graph shown above, when x tends to 2 from its right side, f(x) tends to +∞.

Therefore,

                                       lim     f(x) = +∞
                                    x--> 2⁺

15. Answer :

                                       lim     f(x)
                                    x--> 2

We have to evaluate two-sided limit of f(x) as x tends to 2.

From the answers (13 and 14) above, we have

                           lim     f(x)   ≠   lim     f(x)
                           x--> 2^-              x--> 2⁺

Since, the left-sided limit and right sided limit are not equal, two-sided limit does not exist.

That is,

                           lim     f(x) does not exist
                        x--> 2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.