EVALUTING NUMERIC EXPRESSIONS INVOLVING RATIONAL EXPONENTS

To evaluate numeric numeric values with rational exponents, we follow the steps given below.

Step 1 :

Express the base in exponential form.

Step 2 :

If we have power raised to another power, we will multiply the powers.

Step 3 :

Do possible simplification.

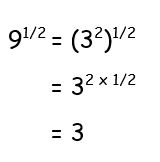
Evaluate the following :

Example 1 :

81^1/2

Solution :

= 81^1/2

Base = 81 and exponent = 1/2

81 = 9²

81^1/2 = (9²)^1/2

= 9^{(2 x 1/2)}

81^1/2 = 9

Example 2 :

16^3/2

Solution :

= 16^3/2

Base = 16, exponent = 3/2

16 = 4²

= 4^{(2 x 3/2)}

= 4³

16^3/2 = 64

Example 3 :

10000^3/4

Solution :

= 10000^3/4

Base = 10000 and exponent = 3/4

10000 = 10⁴

= 10^{(4 x 3/4)}

= 10³

= 1000

Example 4 :

64^2/3

Solution :

= 64^2/3

Base = 64 and exponent = 2/3

64 = 4³

= 4^{(3 x 2/3)}

= 4²

= 16

Example 5 :

27^2/3

Solution :

= 27^2/3

Base = 27 and exponent = 2/3

27 = 3³

= 3^{(3 x 2/3)}

= 3²

= 9

Example 6 :

81^-3/2

Solution :

= 81^-3/2

Base = 81 and exponent = -3/2

81 = 9²

= 9 ^{2 x (-3/2)}

= 9^-3

= 1/9³

= 1/729

Example 7 :

If c^2/5 = 4, then c = ?

Solution :

c^2/5 = 4

Raising power 5 on both sides.

(c^2/5)⁵ = 4⁵

c^{(2/5) x 5} = 4⁵

c² = 4⁵

Take square roots on both sides.

c = √4⁵

c = 4x4√4

c = 16√(2x2)

c = 16(2)

c = 32

Example 8 :

27^4/x = 81, x = ?

Solution :

27^4/x = 81

Try to express the bases 27 and 81 as a multiple of 3.

3³ = 27 and 3⁴ = 81

3^3(4/x) = 3⁴

3^12/x = 3⁴

Since the bases are equal, we can equate the powers.

12/x = 4

Take reciprocal on both sides.

x/12 = 1/4

Multiply 12 on both sides.

x = 12/4

x = 3

Example 9 :

20^1/2 ⋅ 20^1/2

Solution :

20^1/2 ⋅ 20^1/2

Using the property a^m ⋅ aⁿ = a^m+n

= 20^1/2 ⋅ 20^1/2

= 20^{(1/2 + 1/2)}

= 20

Example 10 :

5^1/3 ⋅ 25^1/3

Solution :

= 5^1/3 ⋅ 25^1/3

25 = 5²

= 5^1/3 ⋅ (5²)^1/3

= 5^1/3 ⋅ 5^2/3

= 5^(1+2)/3

= 5^3/3

= 5

Apart from the stuff given above,  if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.