EXAMPLE PROBLEMS OF ANGLE OF ELEVATION AND DEPRESSION

Example 1 :

A boy standing on the ground, spots a balloon moving with the wind in a horizontal line at a constant height . The angle of elevation of the balloon from the boy at an instant is 60°. After 2 minutes, from the same point of observation, the angle of elevation reduces to 30°. If the speed of wind is 29√3 m/min. then, find the height of the balloon from the ground level.

Solution :

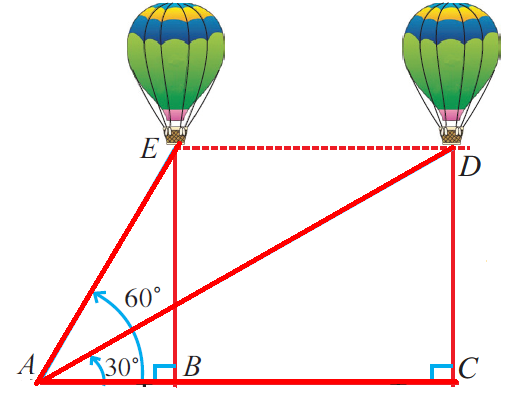
Distance covered by the balloon  =  BC

BC = Time x Speed ==> 2 x 29 √3 ==> 58√3 m

AB = x  then AC = x + 58√3

In triangle DAC :

∠DAC  =  30°

  tan θ = opposite side/Adjacent side

tan 30°  =  DC/AC

1/√3  =  DC/(x + 58√3)

DC = (x + 58√3)/√3 ----(1)

In triangle EAB :

∠EAB  =  60°

  tan θ = opposite side/Adjacent side

tan 60°  =  EB/AB

√3  =  EB/x

x√3  =  EB

 EB  =  √3x ---->(2) 

Since EB = DC

(1) = (2)

(x + 58√3)/√3  =  √3x

 x + 58√3  =  3x

3x - x  =  58√3

2x  =  58√3

x  =   58√3/2 ==> 29√3 m

Height of the balloon from ground level EB  =  √3 x

=  29 √3 (√3)

=  29(3) ==> 87 m

Hence height of the balloon from ground level = 87 m.

Example 2 :

A straight highway leads to the foot of a tower . A man standing on the top of the tower spots a van at an angle of depression of 30°. The van is approaching the tower with a uniform speed. After 6 minutes, the angle of depression of the van is found to be 60°. How many more minutes will it take for the van to reach the tower?

Solution :

From the given information, we can draw a rough diagram 

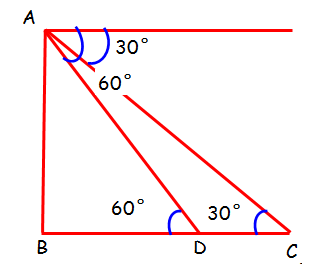
Distance covered by the van to reach D from C = 6 minutes

time taken = x 

Distance between D and C = 6x

In triangle ACB

∠ACB  =  30°

  tan θ = opposite side/Adjacent side

  tan 30° = AB/BC

  1/√3  =  AB/(BD+DC)

1/√3  =  AB/(BD+6x) 

(BD+6x)/√3 = AB ----(1)

In triangle ABD

∠ABD  =  60°

  tan θ = opposite side/Adjacent side

  tan 60° = AB/BD

  √3  =  AB/BD ==> AB  = BD√3  -----(2)

(1) = (2)

(BD+6x)/√3  =  BD√3

BD + 6x = BD(3) 

3BD - BD = 6x

2BD = 6x

BD = 6x /2 = 3x

Here 3 represents number of minutes covered by the van and x stands for time taken.

Hence 3 more minutes will it take for the van to reach the tower.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.