MULTIPLYING POLYNOMIALS WORKSHEET
1) Multiply the following polynomials and find the degree of the resultant polynomial:
(i) p(x) = x2 - 9 and q(x) = 6x2 + 7x - 2
(ii) f(x) = 7x + 2 and g(x) = 15x - 9
(iii) h(x) = 6x2 - 7x + 1 and f(x) = 5x - 7
2) The cost of a chocolate is Rs. (x + y) and Amir bought (x + y) chocolates. Find the total amount paid by him in terms of x and y. If x = 10, y = 5 find the amount paid by him.
3) The length of a rectangle is (3x+2) units and it’s breadth is (3x–2) units. Find its area in terms of x. What will be the area if x = 20 units.
4) p(x) his a polynomial of degree 1 and q(x) is a polynomial of degree 2. What kind of the polynomial p(x) × q(x) is ?

Detailed Answer Key
Answer (1)(i) :
p(x) ⋅ q(x) = (x2 - 9)(6x2 + 7x - 2)

= 6x4 + 7x3 - 56x2 - 63x + 18
Degree of the resultant polynomial is 4.
Answer (1)(ii) :
f(x) ⋅ g(x) = (7x + 2)(15x - 9)

= 105x2 - 33x - 18
Degree of the resultant polynomial is 2.
Answer (1)(iii) :
h(x) ⋅ f(x) = (6x2 - 7x + 1)(5x - 7)
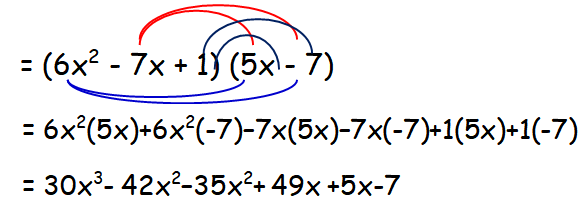
= 30x3 - 77x2 + 54x - 7
Degree of the resultant polynomial is 3.
Answer (2) :
In order to find the total amount paid by him, we have to multiply the cost of 1 chocolate by the number of chocolate he buys.
Cost of 1 chocolate = x + y
Number of chocolates he buys = x + y
Total amount = (x + y) (x + y)
= (x + y)2 ---(1)
= x2 + 2xy + y2
By applying the values of x and y, we get
= (10 + 5)2
= 152
= 225
Hence he has to pay Rs. 225.
Answer (3) :
Length of the rectangle = 3x + 2
Breadth of the rectangle = 3x - 2
Area of rectangle = (3x + 2)(3x - 2)
= 9x2 - 6x + 6x - 4
= 9x2 - 4
If x = 20
Area of rectangle = 9(20)2 - 4
= 9(400) - 4
= 3600 - 4
= 3596
Answer (4) :
The degree of the polynomial p(x) is 1
Degree of the polynomial q(x) is 2.
The product of polynomial is 3.
Hence it is a cubic polynomial.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 101)
Jan 26, 25 07:59 PM
Digital SAT Math Problems and Solutions (Part - 101) -
AP Calculus AB Problems with Solutions (Part - 7)
Jan 26, 25 06:56 AM
AP Calculus AB Problems with Solutions (Part - 7) -
Digital SAT Math Problems and Solutions (Part - 103)
Jan 25, 25 01:00 AM
Digital SAT Math Problems and Solutions (Part - 103)