EXAMPLE PROBLEMS ON POWERS OF IMAGINARY UNIT I

Question 1 :

Simplify the following :

i¹⁹⁴⁷ + i¹⁹⁵⁰

Solution :

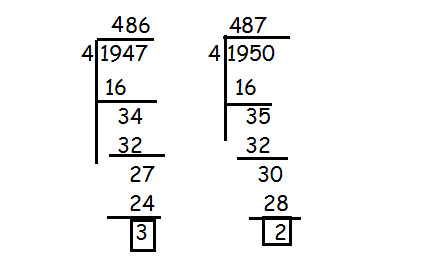
i¹⁹⁴⁷

By dividing 1947 by 4, we get the remainder 3.

So, the value of i¹⁹⁴⁷ is -i

i ¹⁹⁵⁰

By dividing 1950 by 4, we get the remainder 2.

So, the value of i¹⁹⁵⁰ is -1

i¹⁹⁴⁷ + i ¹⁹⁵⁰  =  -i - 1

i¹⁹⁴⁷ + i ¹⁹⁵⁰  =  -i - 1

Question 2 :

Simplify the following :

i¹⁹⁴⁸ - i^-1869

Solution :

i¹⁹⁴⁸ - i^-1869  =  1 - (1/i)

  =  [(i - 1)/i] [i/i]

  =  (i² - i)/i²

  =  (-1 - i)/(-1)

  =  1 + i

Question 3 :

Simplify the following :

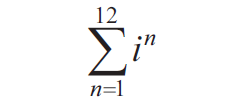
Solution :

If n = 1, then iⁿ  =  i¹  =  i

If n = 2, then iⁿ  =  i²  =  -1

If n = 3, then iⁿ  =  i³  =  i

If  = 4, then iⁿ  =  i⁴  =  1

  =  i + i² + i³ + i⁴ + ...................... + i¹²

  =  (i - 1 + i + 1) + ...................... + i¹²

The above series will have 12 elements, it can be divided into three equal groups.

Each group will contain the above four elements. Hence the answer is 0.

Question 4 :

Simplify the following :

i⁵⁹ + (1/i⁵⁹)

Solution :

=  i⁵⁹ + (1/i⁵⁹) 

By dividing 59 by 4, we get 3 as remainder.

  =  -i + (1/(-i))

  =  -i - (1/i)

  =  -i² - 1

  =  -(-1) - 1

  =  1 - 1  

  =  0

Question 5 :

Simplify the following :

i i² i³ .............i²⁰⁰⁰

Solution :

i i² i³ .............i²⁰⁰⁰

  =  i ^{(1 + 2 + 3 +..............+ 2000)}

  =  i ^{(1 + 2 + 3 +..............+ 2000)}

n = 2000, a = 1, Sn  =  (n/2)[a + l]

  S₂₀₀₀  =  (2000/2) [1 + 2000]

  =  1000 [2001]

  =  2001000

  =  i ^2001000

The power is 2001000 is exactly divisible by 4, we get 0 as remainder.

Hence the answer is 1.

Question 6 :

Simplify the following :

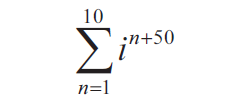
Solution :

If n = 1, then i^{n + 50}  =  i⁵¹

If n = 2 , then i^{n + 50}  =  i^52..........

If n = 10 , then i^{n + 50}  =  i⁶⁰

  =  i⁵¹ + i⁵²+ i^{53 + ............... +} + i⁶⁰

=  i⁵¹ [1 + i + i² + i³ + i⁴ + i⁵ + i⁶ + i⁷ + i⁸ + i⁹ + i¹⁰]

By grouping the first and the next four terms, we get 0.

  =  -i [i - 1]

  =  -i² + i

  =  1 + i

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.