EXAMPLE PROBLEMS ON PROPERTIES OF DEFINITE INTEGRALS

Property 1 :

Integration is independent of change of variables provided the limits of integration remain the same.

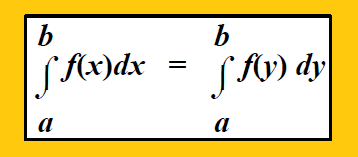
Property 2 :

If the limits of definite integral are interchanged, then the value of integral changes its sign only.

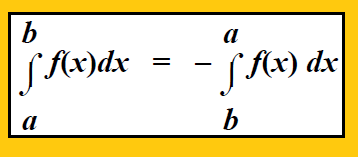
Property 3 :

Property 4 :

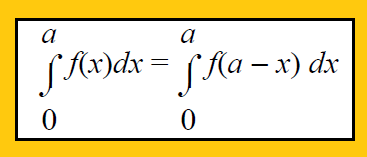
Property 5 :

If f(x) is integrable on a closed interval containing the three numbers a, b and c, then regardless of the order of a, b and c.

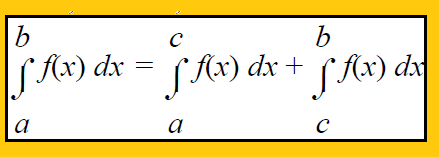
Property 6 :

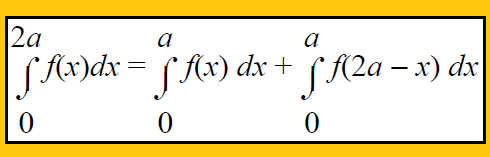
Property 7 :

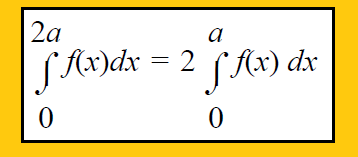
Property 8 :

To check if the function is odd or even, in the given function f(x) apply x  =  -x

• If f(-x)  =  f(x), then f(x) is even.
• If f(-x)  =  -f(x), then f(x) is odd.

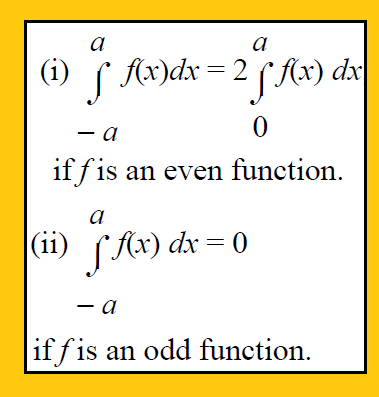
Examples on Properties of Integrals

Example 1 :

Solution :

Let  

Let f(x) = 1/(1 + sin x)

Using the property,

f(a - x) = f(π - x) = 1/(1 + sin (π - x))

= 1/(1 + sin x)

From this, we know that 

f(a - x) = f(x)

Using the property,

Using property,

Example 2 :

Solution :

Let f(x) = x cos x

Since the upper limit and lower limit both are numerically equal except the sign. We have to check if it is odd or even function.

Applying x as -x, we get

f(-x) = -x cos (-x)

= -x cos x

= -[x cos x]

f(-x) = -f(x)

From this, we understand that the given function is odd function. So, its value will become 0.

Example 3 :

Solution :

Let f(x) = e^-|x|

By considering the limits in the given integral, both upper and lower limit are the same and the sign alone differs. Then, we have to check if the given function is odd or even.

Let us apply -x for x,

f(-x) = e^-|x|

= e^-|x|

f(-x) = f(x)

After applying -x, we get the same function. Then it is even function.

Example 4 :

Solution :

Let I = f(x) / f(x) + f(a - x) -----(1)

Applying the property, x should be replaced by a - x

I = f(a - x) / f(a - x) + f(a - (a - x))

= f(a - x) / f(a - x) + f(a - a + x)

= f(a - x) / f(a - x) + f(x) -----(2)

(1) + (2)

Example 5 :

Prove that

Solution :

Let I = 

Using property,

Distributing integrals, we get

Example 6 :

Prove that

Solution :

Let I = integral 0 to 1 [tan^-1 x+ tan^-1 (1 - x)] dx -----(1)

Applying the property of integral, we get

I = integral 0 to 1 [tan^-1 (1-x) + tan^-1 (1 - (1-x))] dx

= integral 0 to 1 [tan^-1 (1-x) + tan^-1 (1 - 1 + x)] dx

= integral 0 to 1 [tan^-1 (1-x) + tan^-1 (x)] dx -----(2)

Even after using the property, we get the same terms. So, let us separate the integrals and use property

= integral 0 to 1 tan^-1 (1-x) dx + integral 0 to 1tan^-1 (x) dx

= integral 0 to 1 tan^-1 (1-(1-x)) dx + integral 0 to 1tan^-1 (x) dx

= integral 0 to 1 tan^-1 (x) dx + integral 0 to 1 tan^-1 (x) dx

= 2 integral 0 to 1 tan^-1 (x) dx

Now using partial derivative, we can integrate the above.

u =  tan^-1 (x) and dv = dx

u'= 1/1+x² and v = x

Using the formula integral u dv = uv - integral v du

Using substitution method, we can find the antiderivative.

Let t = 1 + x²

dt = 2x dx

x dx = dt/2

When x = 0, t = 1 + 0 ==> 1

When x = 1, t = 1 + 1 ==> 2

Example 7 :

Evaluate 

Solution :

Let I = integral 2 to 3 [√x / √(5 - x) + √x] dx ---(1)

Using the property,

= integral 2 to 3 [√(5-x) / √(5 - (5-x)) + √(5-x)] dx

= integral 2 to 3 [√(5-x) / √x + √(5-x)] dx ----(2)

(1) + (2)

2I = integral 2 to 3 [√x + √(5-x)] / [√x + √(5-x)] dx

2 I =  Integral 2 to 3 dx

2I = x (applying the limits)

2I = 3 - 2

2I = 1

I = 1/2

So, the answer is 1/2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.