EXAMPLE PROBLEMS USING ANGLE BISECTOR THEOREM

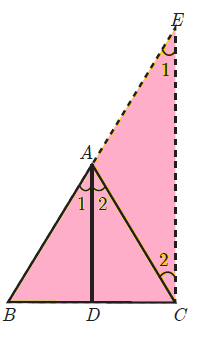
Angle Bisector Theorem :

The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the corresponding sides containing the angle.

In ΔABC, AD is the internal bisector

AB/AC  =  BD/CD

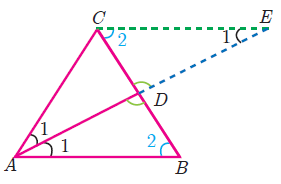
Converse of Angle Bisector Theorem :

If a straight line through one vertex of a triangle divides the opposite side internally in the ratio of the other two sides, then the line bisects the angle internally at the vertex.

ABC is a triangle. AD divides BC in the ratio of the sides containing the angles <A to meet BC at D.

That is AB/AC  =  BD/DC

Example 1 :

In ΔABC, AD is the bisector of ∠A meeting side BC at D, if AB = 10 cm, AC = 14 cm and BC = 6 cm, find BD and DC

AB/AC   =   DB/CD

Let DB  =  x, then CD  =  6 - x

10/14  =  x/(6-x)

5/7  =  x/(6-x)

5(6 - x)  =  7x

30 - 5x  =  7x

7x + 5x  =  30

12x  =  30

x  =  30/12  =  5/2  =  2.5

BD  =  2.5 cm and CD  =  6 - 2.5  =  3.5 cm

Example 2 :

Check whether AD is bisector of ∠A of ΔABC in each of the following 

(i) AB = 5 cm, AC = 10 cm, BD = 1.5 cm and CD = 3.5 cm.

Solution :

By angle bisector theorem :

AB/AC   =   DB/CD

5/10  =  1.5/3.5

1/2  =  3/7

Hence AD is not the bisector of <A.

(ii) AB = 4 cm, AC = 6 cm, BD = 1.6 cm and CD = 2.4 cm.

Solution :

By angle bisector theorem :

AB/AC   =   DB/CD

4/6  =  1.6/2.4

2/3  =  2/3

Hence AD is the bisector of <A.

Example 3 :

In figure <QPR = 90° , PS is its bisector. If ST ⊥ PR,  prove that ST × (PQ + PR) = PQ × PR.

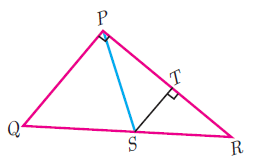
Solution :

Example 4 :

ABCD is a quadrilateral in which AB=AD, the bisector of  <BAC and <CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF  BD .

Solution :

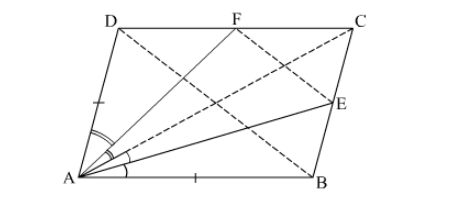
In triangle ABC, AE is the bisector of <BAC

AC/AB  =  CE/BE  ----(1)

In triangle ACD, AF is the bisector <CAD

AC/AD  =  CF/FD

AC/AB  =   CF/FD  ----(2)

(1)  =  (2)

CE/BE  =  CF/FD

Hence EF is parallel to BD.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.