EXAMPLES OF BASIC PROPORTIONALITY THEOREM

Example 1 :

In the figure AP = 3 cm, AR = 4.5 cm, AQ = 6 cm, AB = 5 cm and AC = 10 cm. Find the length of AD.

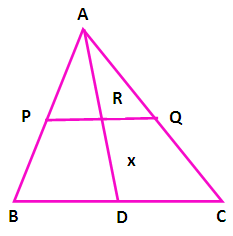
Solution :

From the given information we get, AB/AP = AC/AQ.

In triangle ABC,

AB/AP = AC/AQ

By using converse of “Thales theorem” PQ is parallel to BC.

RD = x

In triangle ABD, PR is parallel to BD

AD = AR + RD

AD  =  4.5 + x

AB/AP  =  AD/AR

5/3  =  (4.5 + x)/4.5

(5 ⋅ 4.5)/3  =  4.5 + x

7.5  =  4.5 + x

x  =  7.5 – 4.5

x  =  3

Here we need to find the length of AD = 4.5 + x

  =  4.5 + 3

  =  7.5 cm

Example 2 :

E and F are points on the sides PQ and PR respectively, of a triangle PQR. For each of the following cases. Verify EF is parallel to QR.

(i)  PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm

Solution :

First let us draw the picture for the above details

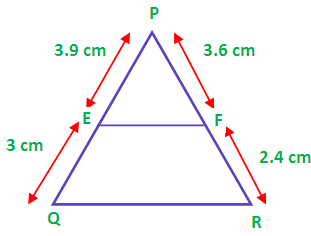
To verify whether EF is parallel to QR we have to check the condition

PE/EQ  =  PF/FR

3.9/3  =  3.6/2.4

1.3 ≠ 1.5

So the sides EF and QR are not parallel.

(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

Solution :

First let us draw the picture for the above details

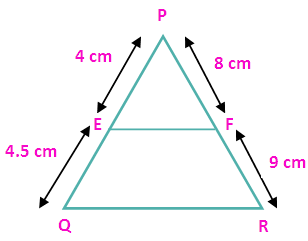
To verify whether EF is parallel to QR we have to check the condition

PE/EQ = PF/FR

4/4.5 = 8/9

0.88 = 0.88

So the sides EF and QR are parallel.

Example 3 :

In the figure, AC is parallel to BD and CF is parallel to DF, if OA = 12 cm, AB = 9 cm, OC = 8 cm and EF=  4.5 cm, then find FQ.

Solution :

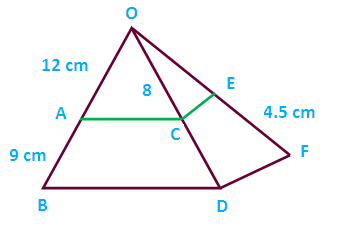
In triangle OBD, AC is parallel to BD. By using “Thales theorem” we get,

OA/AB  =  OC/CD

12/9  =  8/CD

CD  =  (8 x 9)/12

      =  72/12       

 =  6 cm

In triangle ODF, the sides CE and DF are parallel, by using “Thales theorem” we  get,

OC/CD  =  OE/EF

8/6  =  OE/4.5

OE  =  (8 ⋅ 4.5)/6

   =  36/6

   =  6 cm

So, OF = OE + EF

=  6 + 4.5

=  10.5 cm

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.