EXAMPLES OF INTEGRATION BY PARTS

Integration by parts is one of the method basically used o find the integral when the integrand is a product of two different kind of function.                  

Formula :

∫u dv = uv-∫v du

Example 1 :

Evaluate :

∫xe^xdx

Solution :

u  =  x, du  =  dx

dv  =  e^x dx and v  =  e^x 

∫udv  =  uv-∫vdu

=  xe^x-∫e^xdx

=  xe^x-e^x+C

∫ xe^x dx  =  e^x(x-1)+C

Example 2 :

Evaluate :

∫xsinxdx

Solution :

u  =  x, du  =  dx

dv  =  sinx dx and v  =  -cosx 

∫udv  =  uv-∫vdu

=  x(-cosx)-∫(-cosx)dx

=  -xcosx+∫cosxdx

∫ x sin x dx  =   -xcosx + sinx + C

Example 3 :

Evaluate :

∫xlogxdx

Solution :

u  =  logx, du  =  (1/x) dx

dv  =  dx and v  =  x²/2

∫udv  =  uv-∫vdu

=  log x(x²/2) - ∫(x²/2)⋅(1/x)dx

=  log x(x²/2) - (1/2)∫xdx

=  log x(x²/2) - (1/2)(x²/2) + C

∫ x log x dx  =  (x²/2)log x - (x²/4) + C

Example 4 :

Evaluate :

∫xsec²xdx

Solution :

u  =  x, du  =  dx

dv  =  sec²x and v  =  tan x

∫udv  =  uv-∫vdu

=  x(tan x) - ∫tan x dx

∫ xsec²x dx=  x tanx - ln(secx) + C

Example 5 :

Evaluate :

∫xtan^-1xdx

Solution :

u  =  x, du  =  (x²/2)dx

dv  =  tan^-1 x dx and v  =  1/(1+x²)

∫udv  =  uv-∫vdu

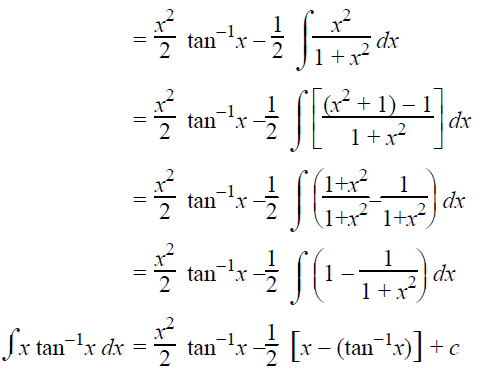
Example 6 :

Evaluate :

∫logxdx

Solution :

u  =  logx , du  =  1/x

dv  =  dx and v  =  x

∫udv  =  uv-∫vdu

=  logx(x) - ∫xdx

∫ log x dx  =  xlogx - (x²/2) + C

Example 7 :

Evaluate :

∫sin^-1xdx

Solution :

u  =  sin^-1x , du  =  1/√(1-x²) dx

dv  =  dx and v  =  x

∫udv  =  uv-∫vdu

=  xsin^-1x-∫x (1/√(1-x²)) dx

=  xsin^-1x-∫ (x/√(1-x²)) dx

Here we may use substitution method to find integration.

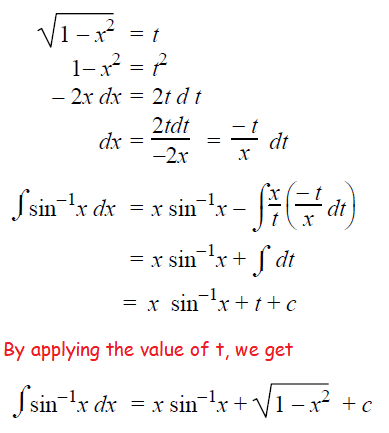
Example 8 :

Evaluate :

∫xsin²xdx

Solution :

sin²x  =  (1-cos2x)/2

∫x sin²x dx  =  ∫x (1-cos2x)/2 dx

=  (1/2)[∫x(1-cos2x) dx]

=  (1/2)[∫x dx - ∫x cos2x dx]

=  (1/2)[(x²/2) - ∫x cos2x dx]  ---(1)

Integrating x cos2x :

u  =  x and du  =  dx

dv  =  cos 2x and v  =  sin2x/2

∫udv  =  uv-∫vdu

=  x(sin2x/2)-∫(sin2x/2) dx

=  (x/2)sin2x-(1/2)∫sin2x dx

∫x cos2x dx  =  (x/2)sin2x+(1/4)cos 2x

Applying the integrated answer in (1), we get

=  (1/2)(x²/2) - 1/2[(x/2)sin2x+(1/4)cos 2x] + C

=  (x²/4) - (x/4)sin2x-(1/8)cos 2x + C

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.