EXAMPLES ON MATRIX EQUALITY

Example 1 :

If

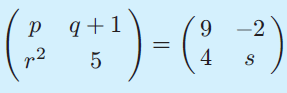
find p, q, r and s.

Solution :

Both are 2x 2 matrices, so they are equal and their corresponding terms will be equal.

By equating corresponding terms, we get

So, the values of p, q, r and s are 9, -3, ±2 and 5 respectively.

Example 2 :

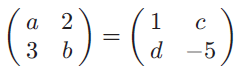
Solution :

By equating corresponding terms, we get

a  =  1, b  =  -5, c  =  2 and d  =  3.

Example 3 :

Solution :

By equating corresponding terms, we get

x  =  -2

a  =  5

2a  =  b

By applying the value of a in 2a  =  b, we get 

2(5)  =  b

b  =  10

So, the value of x is -2, a  =  5 and b  =  10.

Example 4 :

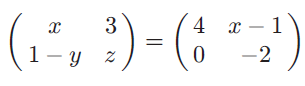
Solution :

By equating corresponding terms, we get

x  =  4

1-y  =  0

y  =  1

z  =  -2

So, the value of x is 4, y  =  1 and z  =  -2.

Example 5 :

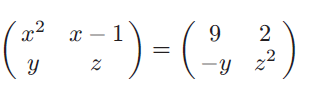
Solution :

x²  =  9

x  =   ±3 

But equating x-1 to 2, we get

x  =  3

So, the value of x is 3, y = 0 and z  =  0 or 1.

Example 6 :

Solution :

By multiplying 1 x 2 by 2 x 2, we get 1 x 2 matrix.

= [2x-9     4x + 0]

= [2x - 9      4x]

Now we have to multiply 1 x 2 by 2 x 1, we get 1 x 1 matrix.

= x(2x - 9) + 8(4x)

= 2x² - 9x + 32x

= 2x² + 23x

2x² + 23x = 0

x(2x + 23) = 0

x = 0 and 2x = -23

x = -23/2

So, the required values of x are 0 and -23/2.

Example 7 :

Solution :

All three matrices are with the same order, 2 x 2. By combining the corresponding terms, we get

2 - 4 = x -----(1)

2 - (-1) = y -----(2)

6 - 5 = z ------(3)

From (1), -2 = x, then x = -2

From (2), 2 + 1 = y, then y = 3

From (3), 6 - 5 = z, then z = 1

So, the values of x, y and z are -2, 3 and 1 respectively.

Example 8 :

Solution :

By equating the corresponding terms, we get

2 = 4x - 6

4x = 2 + 6

4x = 8

x = 8/4

x = 2

So, the required value of x is 2.

Example 9 :

Solution :

Solving for b,

4b + 2 = 11

4b = 11 - 2

4b = 9

b = 9/4

Solving for c,

-3 = -2c - 1

-3 + 1 = -2c

-2c = -2

c = 1

Solving for d,

 4d = 0

d = 0/4

d = 0

Solving for a,

-4a = -8

a = 8/4

a = 2

Solving for f,

2f - 1 = 0

2f = 1

f = 1/2

Solving for g,

-14 = -3g - 2

-14 + 2 = -3g

-3g = -12

g = 12/3

g = 4

So, the values of a = 2, b = 9/4, c = 1, d = 0, f = 1/2 and g = 4.

Example 10 :

Solution :

4c = 2c + 5

4c - 2c = 5

2c = 5

c = 5/2

Solving for d,

2 - d = 4d

2 = 4d + d

5d = 2

d = 2/5

solving for h,

By comparing the corresponding terms, h = -1

Solving for g, 

By comparing the corresponding terms, we get

g = 5

Solving for f,

f - g = 2

By applying the value of g, we get

f - 5 = 2

f = 2 + 5

f = 7

Solving for c,

-10 = -4c

c = 10/4

c = 5/2

Example 11 :

Find the values of a and b if A = B where 

Solution :

By equating the corresponding terms, we get

-6 = b² - 5b

b² - 5b + 6 = 0

(b - 3)(b - 2) = 0

b = 3 and b = 2

So, the value of a = 2 and the values of b are 1, 2, 3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.