EXPECTED VALUE OF A CONTINUOUS RANDOM VARIABLE

Expected value or Mathematical Expectation or Expectation of a random variable may be defined as the sum of products of the different values taken by the random variable and the corresponding probabilities.

For example, if a continuous random variable takes all real values between 0 and 10, expected value of the random variable is nothing but the most probable value among all the real values between 0 and 10.   

That is, the value which has more chance to occur.

Let "x" be a continuous random variable which is defined in the interval (-∞ , +∞) with probability density function f(x). 

Then, the expected value is given by 

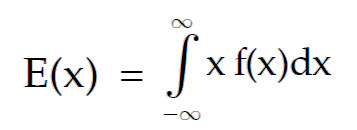
Expected value of x² is given by

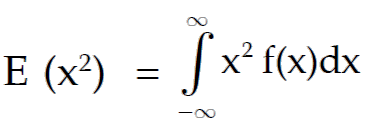
Note :

Expected value is also called as mean

Properties of Expected Value

1.  Expectation of a constant k is k

That is,

E(k) = k for any constant k

2.  Expectation of sum of two random variables is the sum of their expectations.

That is,

E(x + y) = E(x) + E(y) for any two random variables x and y.

3.  Expectation of the product of a constant and a random variable is the product of the constant and the expectation of the random variable.

That is, 

E(kx)  =  k.E(x) for any constant k

4. Expectation of the product of two random variables is the product of the expectation of the two random variables, provided the two variables are independent.

That is,

E(xy)  =  E(x).E(y)

Whenever x and y are independent.

Examples

Example 1 :

In a continuous distribution, the probability density function of x is

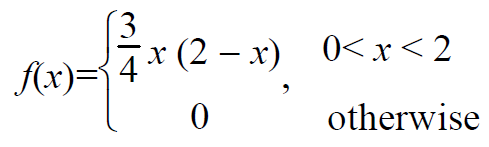
Find the expected value of x. 

Solution :

Expected value of x is given by 

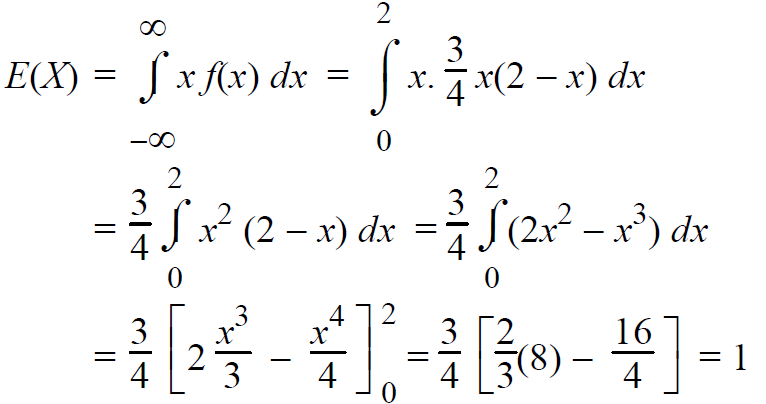
Therefore, the expected value of x is 1.

Example 2 :

In a continuous distribution, the probability density function of x is

Find the expected value of x. 

Solution :

Expected value of x is given by 

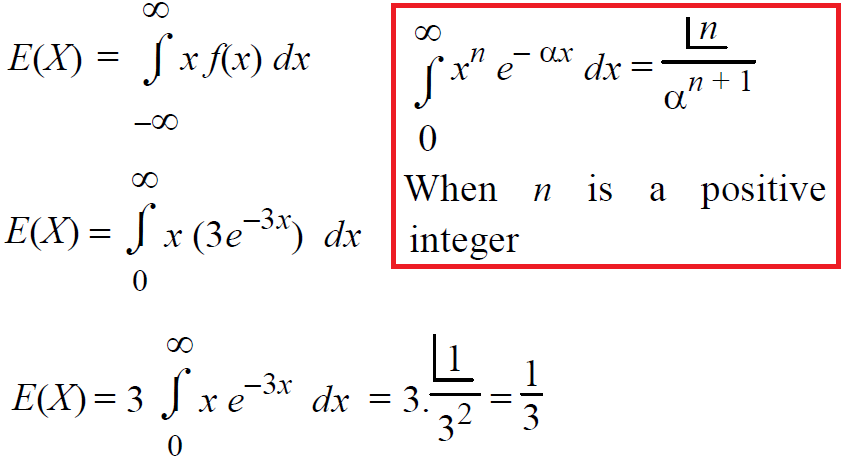
Therefore, the expected value of x is 1/3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.