EXPERIMENTAL AND THEORICAL PROBABILITY WORKSHEET

Experimental Probability - Practice Questions

Problem 1 :

Find the experimental probability of 

(a)  Tossing a head with one toss of a coin if it falls heads 96 times in 200 tosses.

(b) Rolling a six with a die given that when it was rolled 300 times, a six occurred 54 times

Solution

Problem 2 :

Find the experimental probability of rolling an odd number with a die if an odd number occurred 33 times when the die was rolled 60 times.             Solution

Problem 3 :

Clem fired 200 arrows at a target and hit the target 168 times. Find the experimental probability of Clem hitting the target.             Solution

Problem 4 :

Ivy has free-range hens. Out of the first 123 eggs that they laid she found that 11 had double-yolks. Calculate the experimental probability of getting a double-yolk egg from her hens.            Solution

Problem 5 :

Jackson leaves for work at the same time each day. Over a period of 227 working days, on his way to work he had to wait for a train at the railway crossing on 58 days. Calculate the experimental probability that Jackson has to wait for a train on his way to work.

Solution

Problem 6 :

Ravi has a circular spinner marked P, Q and R on equal sectors. Find the experimental probability of getting a Q if the spinner was twirled 417 times and finished on Q on 138 occasions.

Solution

Problem 7 :

Each time Claude shuffled a pack of cards before a game, he recorded the suit of the top card of the pack His results for 140 games were 34 Hearts, 36 Diamonds, 38 Spades and 32 Clubs.

Find the experimental probability that the top card of a shuffled pack is :

(a) a Heart  (b) a Club or Diamond

Solution

Problem 8 :

If a car factory checks 360 cars and 8 of them have defects, how many will have defects out of 1260?

Solution

Problem 9 :

If a car factory checks 320 cars and 12 of them have defects, how many out of 560 will NOT have defects?

Solution

Problem 10 :

What is the theoretical probability that an even number will be rolled on a number cube?

Solution

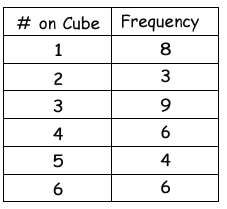
Problem 11 :

What was the experimental probability of how many times an even number was actually rolled using the table?

Solution

Problem 12 :

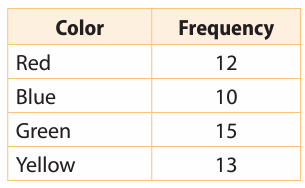
Martin has a bag of marbles. He removed one marble at random, recorded the color and then placed it back in the bag. He repeated this process several times and recorded his results in the table. Find the experimental probability of drawing each color.

Solution

Theoretical Probability

Problem 1 :

A die is rolled. What is the theoretical probability of getting :

a) a "six"

b) a "prime number"?

Solution

Problem 2 :

A bag contains 1 yellow, 2 green and 5 blue beds. One bead is chosen at random. Find the probability that it is :

(a)  Yellow  (b)  not yellow

Solution

Problem 3 :

1 A die numbered 1 to 6 is rolled once. Find:

a) P(3)

b) P(even number)

c) P(a number at least 1)

d) P(5)

e) P(not a 5)

f) P(a number greater than 6)

Solution

Problem 4 :

The five illustrated cards are well shuffled and placed face down on a table. One of the cards is randomly chosen. 

Solution

Problem 5 :

A bag contains 10 beads. 5 are white, 2 are red, 1 is blue, 1 is green and 1 is black. A bead is taken at random from the bag. Find:

a) P(white)

b) P(blue)

c) P(not black)             Solution

Problem 6 :

A letter is randomly chosen from GENEVA.

a)  Find the probability that it is:

(i) an E

(ii) a Z

b) Given that the letter chosen first is a G and it is removed, what is the probability that a second randomly chosen letter is a vowel?          Solution

Problem 7 :

A dart board has 30 sectors, numbered 1 to 30. A dart is thrown towards the bulls-eye and misses in a random direction. Determine the probability that the dart hits:

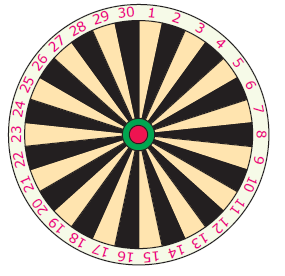
a) a multiple of 5

b) a number between 7 and 13 inclusive

c) a number greater than 18

d) 15

e) a multiple of 7

f) an even number that is a multiple of 3.

Solution

Problem 8 :

A shoebox holds a number of disks of the same size. There are 5 red, 6 white, and 7 blue disks. You pick out a disk, record its color, and return it to the box. If you repeat this process 250 times, how many times can you expect to pick either a red or white disk?

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.