EXPERIMENTAL PROBABILITY

In such a case, the probability of an event is being determined through an actual experiment. 

Example :

When we toss a coin 10 times, how many times can we get head ? 

When we toss a coin once, the probability of getting head is 1/2. 

Since, there is 50% chance of getting head when a coin is tossed once, we can say that we will get head 5 times out of tossing a coin 10 times.  

Are we 100% sure that we will get head 5 times ? 

Our answer will be "NO". 

When the actual experiment is conducted, the result may vary. 

We may get head 0 times or 1 time or 2 times or 3 times ..........up to 10 times.

In the actual experiment of tossing a coin 10 times, say, we get head 3 times.

Then the probability of getting head is 3/10. 

This is called experimental probability. 

Because, here we find the probability after the experiment was conducted. 

Based on the example explained above, we can get the formula given below to find experimental probability. 

Question 1 : 

David tossed a coin 20 times and received head 12 times and tail 8 times. Find the experimental probability of getting tail. 

Answer : 

Step 1 : 

Find the total no. of trials. 

Total number of trials  =  20

Step 2 : 

Find the no. of times tail received. 

Number of times tail received  =  8

Step 3 : 

Find the probability. 

Experimental probability

= number of times the even occurs/total number of trails

Experimental probability  =  8/20

Simplify.

Experimental probability  =  2/5

Question 2 : 

A dentist has 400 male and female patients that range in ages from 10 years old to 50 years old and up as shown in the table. What is the experimental probability that the next patient will be female and in the age range 22–39 ?

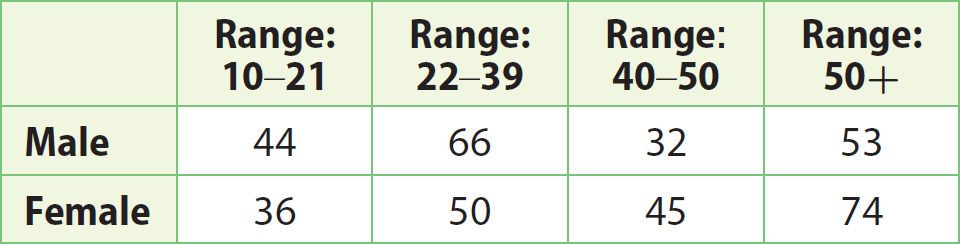
Answer : 

Step 1 : 

Find the total no. of patients. 

Total no. of patients is 

=  44 + 66 + 32 + 53 + 36 + 50 + 45 + 74

=  400

Step 2 : 

Find the no. of female patients in the age range 22 - 39.

No. of female patients in the age range 22 - 39  =  50

Step 3 : 

Find the probability. 

Experimental probability  =  50/400

Simplify.

Experimental probability  =  1/8

Question 3 :

A spinner has three unequal sections: red, yellow, and blue. The table shows the results of Nolan’s spins. Find the experimental probability of landing on each color. Write your answers in simplest form

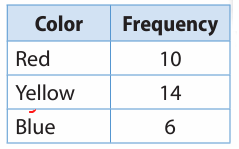
Answer : 

Total number of trails = 10 + 14 + 6

= 30

Probability of landing on red color = 10/30

= 1/3

Probability of landing on yellow color = 14/30

Probability of landing on blue color = 6/30

Question 4 :

A spinner has four sections lettered A, B, C, and D. The table shows the results of several spins. Find the experimental probability of spinning each letter as a fraction in simplest form, a decimal, and a percent.

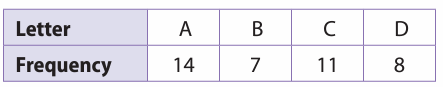
Solution :

Total number of trails = 14 + 7 + 11 + 8

= 40

Probability of getting A = 14/40

Simplest form = 7/20

As decimal = 0.35

As percent = 0.35 x 100%

= 35%

Probability of getting B = 7/40

= 7/40

As decimal = 0.175

As percent = 0.175 x 100%

= 17.5%

Probability of getting C = 11/40

= 11/40

As decimal = 0.275

As percent = 0.275 x 100%

= 27.5%

Probability of getting D = 8/40

= 1/5

As decimal = 0.2

As percent = 0.2 x 100%

= 20%

Question 5 :

Rachel’s free-throw average for basketball is 60%. She wants to predict how many times in the next 50 tries she will make a free throw. 

Solution :

Number of times she make a free throw = 60% of 50

= 0.60(50)

= 30 times

Question 6 :

A food trailer serves chicken and records the order size and sides on their orders, as show in the table. What is the experimental probability that the next order is for 3-pieces with cole slaw?

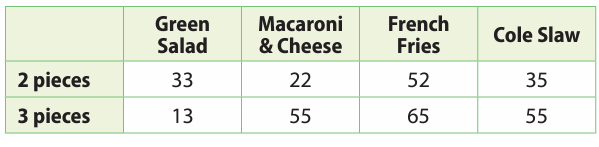
Solution :

Total number trails = 33 + 22 + 52 + 35 + 13 + 55 + 65 + 55

= 330

the number of orders that are for 3 pieces with cole slaw = 55.

Required probability = 55/330

= 1/6

Question 7 :

Drink sales for an afternoon at the school carnival were recorded in the table. What is the experimental probability that the next drink is a small cocoa?

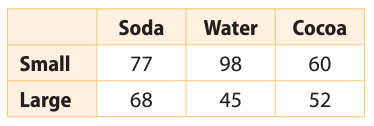
Solution :

Total number sales = 77 + 98 + 60 + 68 + 45 + 52

= 400

Number of small cocoa = 60

Required probability = 60/400

= 3/20

Question 8 :

A jeweler sells necklaces made in three sizes and two different metals. Use the data from a simulation to find the experimental probability that the next necklace sold is a 20-inch gold necklace.

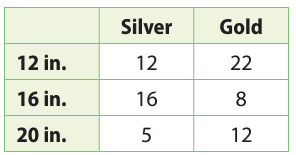
Solution :

Total number of necklaces sold

= 12 + 16 + 5 + 22 + 8 + 12

= 75

Number of necklace sold 20 inch gold necklace = 12

Required probability = 12/75

= 0.16

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.