EXPLORING AREAS OF COMPOSITE FIGURES

In this section, we are going to explore the area of composite figures that are composed of smaller shapes.  

The diagram given below can be a good example of composite figure. This composite figure is made up of two triangles and one rectangle.  

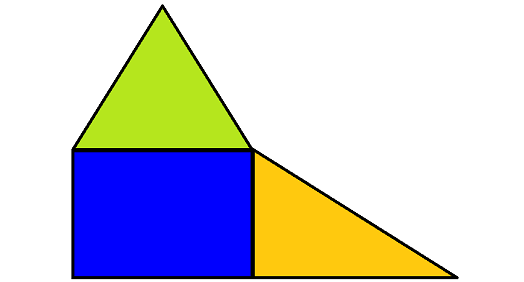
To find the area of a composite figure, separate the figure into simpler shapes whose area can be found. Then add the areas together.

Be sure than none of the simpler figures have overlapping areas. 

Exploring Areas of Composite Figures

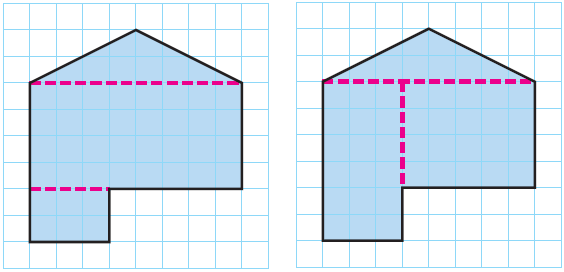
Aaron was plotting the shape of his garden on grid paper. While it was an irregular shape, it was perfect for his yard. Each square on the grid represents 1 square meter.

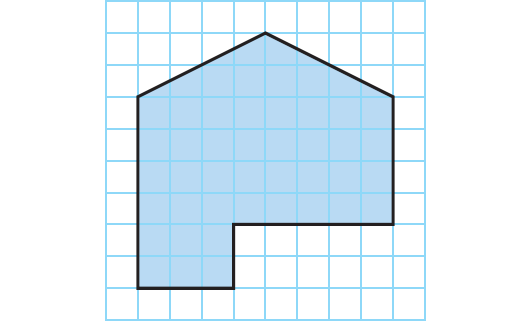
A. Describe one way you can find the area of this garden.

Answer : 

I can divide it into rectangles and triangles, use a formula to find the area of each, and then add the areas together.

B.  Find the area of the garden. 

Answer : 

The area of the garden is 46 square meters.

C.  Compare your results with other students. What other methods were used to find the area?

Answer : 

Other students counted squares; rearranged the triangle to be a rectangle and found the area, and then found the area of the other rectangles in the garden.

D.  How does the area you found compare with the area found using different methods ?

Answer : 

It is the same as the other students.

E.  Use dotted lines to show two different ways Aaron’s garden could be divided up into simple geometric figures.

Answer : 

Finding the Area of a Composite Figure

Find the area of the figure given below. 

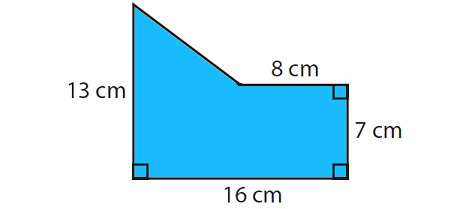
Solution :

By drawing a horizontal line (BD), we can divide the given composite figure into two parts as given below. 

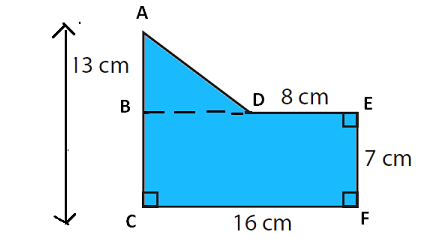
In the above figure,

(1)  BECF is a rectangle

(2) ABD is a triangle

Area of the given composite figure

= Area of rectangle BECF + Area of triangle ABD

Area of rectangle BECF :

length CF = 16 cm and width BC = 7 cm

= length x width 

 =  16 x 7

=  112 cm² ----(1)

Area of triangle ABD :

Base BD  =  BE - DE  =>  16 - 8 => 8 cm

Height AB = AC - BC => 13 - 7 => 6

Area of triangle ABD = (1/2) x b x h

  =  (1/2) x 8 x 6

= 24 cm² ----(2)

(1) + (2) :

Area of the given composite figure is

=  112 + 24

=  136 cm²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.