EXPLORING GRAPHS OF RATIONAL FUNCTIONS

Understanding the graphs of rational functions is sometimes a difficult stuff for some student who study math in both school level and college level. 

Actually, it is not a difficult one. We can understand the graphs of rational functions when we explore them in a proper way. 

To explore the graphs of rational functions, let us consider the example which is given below. 

Rational Function - Example

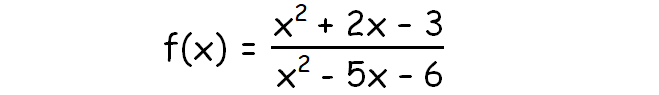
In the process of exploring graphs of rational functions, first we have to know the following stuff. 

1. Vertical Asymptote

2. Horizontal Asymptote

3. Slant Asymptote

4. Hole

To know more about the above mentioned stuff, please click the topics given above.

If you had already learned the above mentioned stuff, then you are ready to learn the stuff, "How to graph rational functions".

Now let us take an example and explore the graphs of rational functions.

Example :

Graph the rational function given below.

y  =  (2x + 1) / (x - 1)

Solution :

Step 1 :

First, we have to find hole, if any.

To find hole of the rational function, we have to see whether there is any common factor found at both numerator and denominator.

In our problem, clearly there is no common factor found at both numerator and  denominator.So, there is no hole.

Step 2 :

Now, we have to find vertical asymptote, if any. 

Most of the rational function will have vertical asymptote. 

To find vertical asymptote, we have to make the denominator equal to zero.

When we do so,    x - 1 = 0  ====>    x  =  1

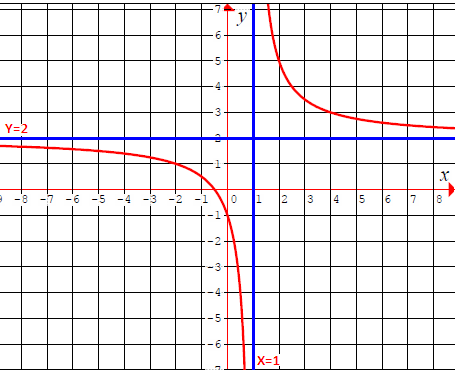
So, the vertical asymptote is   x  =  1

Step 3 :

Now we have to find horizontal asymptote, if any.

In the rational function given above, the highest exponent of the numerator and denominator are equal. So there is an horizontal asymptote. 

Equation of the horizontal asymptote:

y = a/b

Here 'a' and 'b' are the coefficients of highest exponent terms at the numerator and denominator respectively.  

In our problem,   a  =  2  and b  =  1

So, horizontal asymptote is

y  =  2/1

y  =  2

Step 4 :

Now we have to find slant asymptote, if any.

Since there is horizontal asymptote, there is no slant asymptote.

Step 5 :

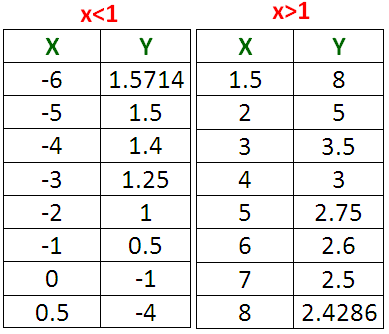
In the given rational function, now we have to plug some random values for x and find the corresponding values of y. 

We have already known that the vertical asymptote is

x  =  1 

Now, we have to take some random values for x on the left side of x = 1 as well as right side of x = 1 (as given in the table below).

That is, 

x < 1 and x > 1 but x ≠ 1

(Because, x = 1 is vertical asymptote)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.