EXPLORING PROPERTIES OF PARENT FUNCTIONS

In mathematics, every function can be classified as a member of a family. Each member of a family of functions is related to the simplest, or most basic, function sharing the same characteristics. This function is called the parent function. 

Exploring the properties of parent functions is trying to know something about it like its graph, name, its family members etc.,

Now, let us look at some different parent functions, their family name, family members and examples. 

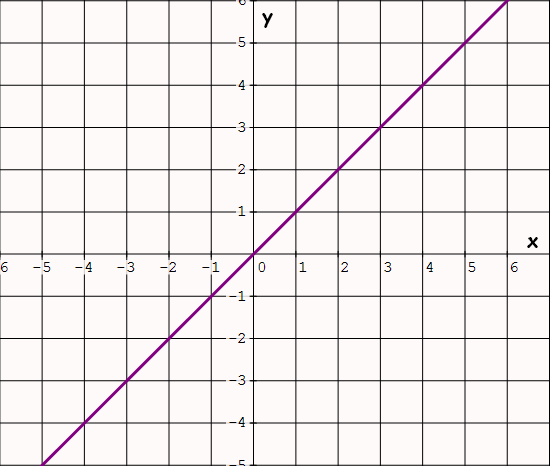
Linear Function

Parent function : f(x) = x

Family members : f(x) = mx + b

Examples : f(x) = 3x + 2, f(x) = -3x + 4

Special features :

(i)  Straight line goes through the origin.

(ii)  Slope is 1.

(iii)  Divides the plane exactly in half diagonally.

(iv)  Graph only quadrants 1 and 3.

Graph of the parent function f(x) = x :

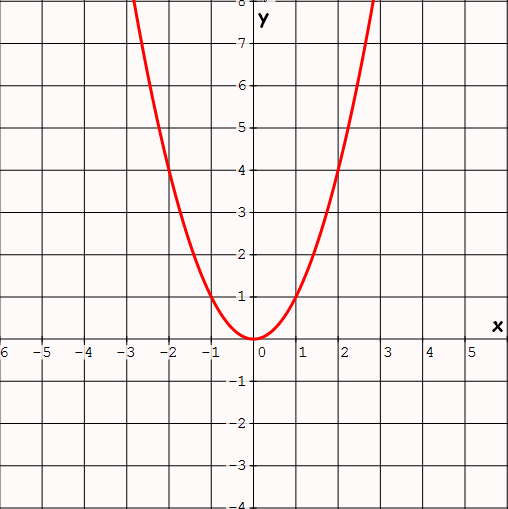
Quadratic Function

Parent function : f(x) = x²

Family members : f(x) = a(x - h)² + k

Examples : f(x) = 5(x - 3)² - 2, f(x) = -x² + 3

Special features :

(i)  Parabola that opens up ward.

(ii)  Vertex at the origin.

(iii)  y has a minimum value.

(iv)  y-axis is axis of symmetry.

(v)  Graph only in quadrants 1 and 2.

Graph of the parent function f(x) = x² :

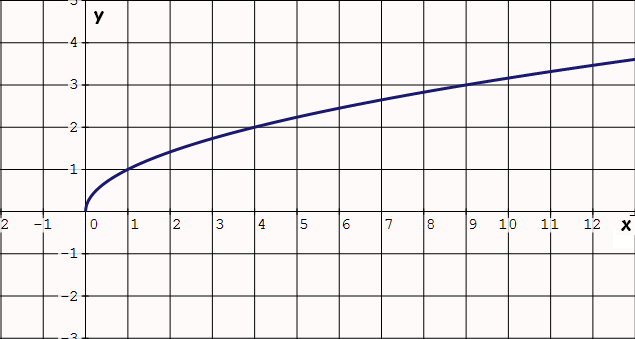
Square Root Function

Parent function : f(x) = √x

Family members : f(x) = a√(x - h) + k

Examples : f(x) = 5√(x - 3) - 2, f(x) = -√x + 3

Special features :

(i)  Semi parabola that opens right ward.

(ii)  Vertex at the origin.

(iii)  x has a minimum value.

(iv)  x-axis is axis of symmetry.

(v)  Graph only in quadrant 1.

Graph of the parent function f(x) = √x :

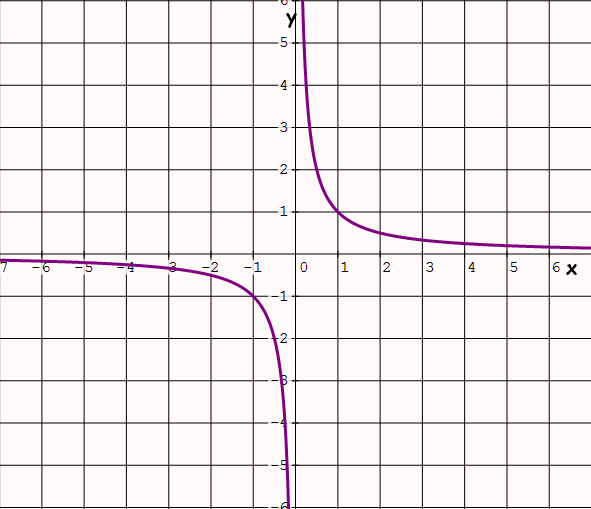
Reciprocal Function

Parent function : f(x) = 1/x

Examples : f(x) = 1/(x - 3), f(x) = 2/(3x + 5)

Special features :

(i)  This curve has two parts.

(ii)  Horizontal asymptote is y = 0.

(iii)  Vertical asymptote is x = 0.

(v)  Graph only quadrants 1 and 3.

Graph of the parent function f(x) = 1/x :

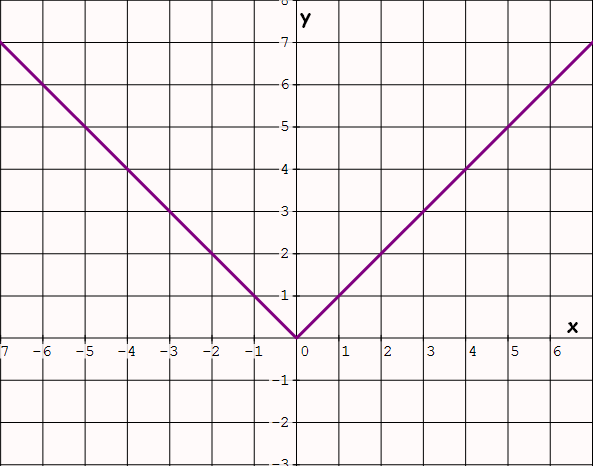
Absolute Value Function

Parent function : f(x) = |x|

Examples : f(x) = 2|x+3|, f(x) =|x| + 5

Special features :

(i)  V-shaped curve and open upward.

(ii)  Vertex at the origin.

(iii)  y has a minimum value.

(iv)  y-axis is axis of symmetry.

(v)  Graph only quadrants 1 and 2.

Graph of the parent function f(x) = |x| :

Identify the function family to which f belongs. Compare the graph of f to the graph of its parent function.

Problem 1 :

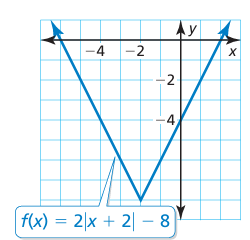
Solution :

f(x) = 2|x + 2| - 8

This is the graph of absolute value function. Comparing with the parent function of absolute value function.

y = |x|

Since,

• 2 is added, then we have to move the graph of parent function left of 2 units.
• 8 is subtracted, then we have to move the graph of parent function moving downwards of 8 units.
• 2 is multiplied, then we have to perform vertical stretch of 2 units.

Problem 2 :

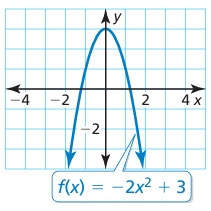
Solution :

f(x) = -2x² + 3

This is the graph of quadratic function. Comparing with the parent function of quadratic function.

y = x²

Since,

• 2 is multiplied then we have to perform the vertical stretch of 2 units. 
• It is multiplied by negative, then the parent function should be reflected with respect to x-axis.
• 3 is added then move the parent graph 3 units up.

Problem 3 :

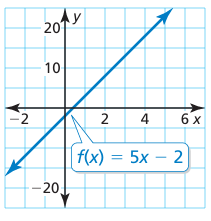
Solution :

f(x) = 5x - 2

This is the graph of linear function. Comparing with the parent function of linear function.

y = x

Since,

• 5 is multiplied, then we have to perform the vertical stretch of 5 units.
• 2 is subtracted, then we have to move the graph of parent function 2 units down.

Problem 4 :

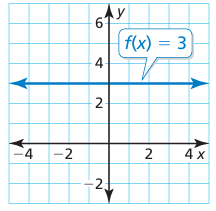
Solution :

f(x) = 3

This is the graph of linear function. Comparing with the parent function of linear function.

y = x

y = 0x + 3

Since,

• 0 is multiplied by x, then it must be the horizontal line.
• 3 is added, then move the graph 3 units to the right.

Compare each function with its parent function. State whether it contains a horizontal translation, vertical translation, both, or neither. Explain your reasoning.

Problem 5 :

f(x) = 2 ∣x∣ − 3

Solution :

Its is absolute value function, it has the following transformations.

Stretch / shrink :

Vertical stretch of 2 units.

Translation :

Vertical translation of 3 units down.

Problem 6 :

f(x) = (x − 8)²

Solution :

It is quadratic function, it has the following transformations.

Stretch / shrink :

No vertical or horizontal stretch or shrink.

Translation :

Horizontal translation of 8 units to the right.

Problem 7 :

f(x) = ∣x + 2∣ + 4

Solution :

Its is absolute value function, it has the following transformations.

Stretch / shrink :

No vertical stretch or shrink.

Translation :

Vertical translation of 4 units up, horizontal translation of 2 units to the left.

Problem 8 :

f(x) = 4x²

Solution :

It is quadratic function, it has the following transformations.

Stretch / shrink :

Vertical stretch of 4 units.

Translation :

No, there is no translation.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.