EXPONENTS AND RADICALS WORKSHEET FOR GRADE 11

(i) For n ∈ N, n even, and b > 0, there is a unique a > 0 such that aⁿ = b.

(ii) For n ∈ N, n odd, b ∈ R, there is a unique a ∈ R such that aⁿ = b. In both cases a is called the nth root of b or radical and is denoted by b^1/n or ⁿ√b

(i) If n = 2, then nth root is called the square root; if n = 3, then it is called cube root.

(ii) Observe that the equation  x² = a², has two solutions x = a, x = −a; but √a² = |a|.

(iii) Properties of exponents given above are still valid for radicals provided each of the individual terms are defined.

(iv) Note that for n ∈ N and a ≠  0 we have

(aⁿ)^1/n  =  |a| if n is even, a if n is odd

Questions

(1) Simplify 

(i)  (125)^2/3                Solution

(ii)   (16)^-3/4         Solution

(iii)  (-1000)^-2/3     Solution

(iv)  (3^-6)^1/3             Solution

(v)   27^-2/3/27^-1/3      Solution

(2)  Evaluate (((256)^-1/2)^-1/4)³           Solution

(3)  Evaluate If (x^1/2 + x^−1/2)² = 9/2, then find the value of (x^1/2 − x^−1/2) for x > 1.        Solution

(4)  Simplify and hence find the value of n: 3²ⁿ9²3⁻ⁿ/3³ⁿ = 27.         Solution

(5)  Find the radius of the spherical tank whose volume is 32π/3 units.      Solution

(6)  Simplify by rationalising the denominator.

(7 + √6) / (3 - √2)         Solution

(7)  Simplify

Solution

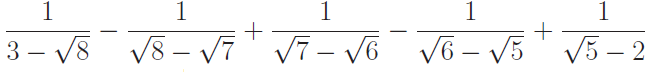
(8)  Simplify

If x = √2 + √3 find (x² + 1)/(x² − 2)    Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.