EXPONENTS WITH NEGATIVE BASES

In solving problems on exponents with negative base, we may have the following  two situations.

(i) Positive exponents with negative bases. 

(ii) Negative exponents with negative bases. 

Negative base will become positive if the power is even. Negative base will become negative if the power is odd.

Whenever we have a negative number as exponent and we need to make it as positive, we have to flip the base that is write the reciprocal of the base and change the negative exponent as positive exponent.

Positive Exponents with Negative Bases

When we do problems on positive exponents with negative bases, it is important to know the difference between

(-3)²   and   -3²

Order of operations (PEMDAS) dictates that parentheses take precedence.

So, we have

(-3)²  =  (-3) ⋅ (-3)

(-3)²  =  9

Without parentheses, exponents take precedence :

-3²  =  -3 ⋅ 3

-3²  =  -9

The negative is not applied until the exponent operation is carried through. We have to make sure that we understand this. So, we will not make this common mistake. 

Sometimes, the result turns out to be the same, as in. 

(-2)³   and   -2³

That is, 

(-2)³  =  (-2)(-2)(-2)  =  -8

(-2)³  =  - 2 ⋅ 2 ⋅ 2  =  -8

Result 1 :

If there is positive even exponent and negative sign inside the parenthesis, then the result is positive. 

Example : 

(-a)²  =  a²

Result 2 : 

If there is positive odd exponent and negative sign inside the parenthesis, then the result is negative. 

Example : 

(-a)²  =  a²

Negative Exponents with Negative Bases

Consider the following exponential form.

(-a)^-b

Here the base is '-a' and the exponent is '-b'.

To evaluate (-a)^-b, first we have to change the negative sign of the exponent as positive shown below. 

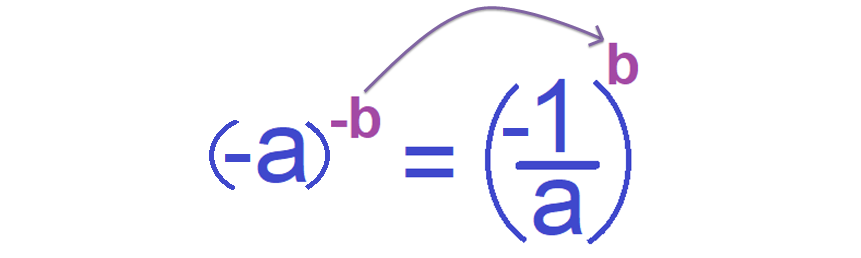
From the above example, it is clear that if there is a negative exponent for a base, the negative exponent can be changed as positive exponent by taking the reciprocal to the base.

We have to do further evaluation based on the exponent (even or odd). 

Solved Problems

Problem 1 :

Evaluate : 

-8²

Solution : 

=  -8²

=  - 8 ⋅ 8

=  - 64

Problem 2 :

Evaluate : 

(-8)²

Solution :

=  (-8)(-8)

=  64

Problem 3 :

Evaluate : 

(-8)³

Solution : 

= (-8)(-8)(-8)

= -512

Problem 4 :

Evaluate : 

-4³

Solution : 

=  - 4 ⋅ 4 ⋅ 4

=  -64

Problem 5 :

Evaluate : 

3^-2

Solution : 

=  3^-2

=  (1/3)²

Distribute the exponent to numerator and denominator. 

=  1² / 3²

=  1/9

Problem 6 :

Evaluate : 

(-3/2)^-2

Solution : 

=  (-3/2)^-2

=  (-2/3)²

Since the exponent is even, the negative sign inside the parentheses will become positive. 

=  (2/3)²

Distribute the exponent to numerator and denominator. 

=  2² / 3²

=  4/9

Problem 7 :

Evaluate : 

(-5/4)^-3

Solution : 

=  (-5/4)^-3

=  (-4/5)³

Since the exponent is odd, the negative sign inside the parentheses will remain same. 

Distribute the exponent to numerator and denominator. 

=  - 4³ / 5³

=  - 64/125

Problem 8 :

Evaluate :

(-5^-2) ⋅ (-3^-4)

Solution :

=  (-5^-2) ⋅ (-3^-4)

=  (-1/5)² ⋅ (-1/3)⁴

=  (1/25) ⋅ (1/81)

=  1/2025

Problem 9 :

Evaluate :

(-3)^-4/ (-2)^-3

Solution :

=  (-3)^-4/ (-2)^-3

=  (-1/3)⁴/ (-1/2)³

=  (1/81) / (-1/8)

=  (1/81) ⋅ (-8/1)

=  - 8/81

Problem 10 :

It is given that (-a)^-1/3  =  4/3. Find the value of a. 

Solution :

(-a)^-1/3  =  4/3

-a  =  (4/3)^-3/1

-a  =  (4/3)^-3

-a  =  (3/4)³

Distribute the exponent to numerator and denominator. 

-a  =  3³ / 4³

-a  =  27/64

Multiply each side by -1. 

a  =  - 27/64

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.