EXPRESSING AS A SINGLE FRACTION

When we add two or more fractions in general, first we will look into the denominators and check if they are same or not.

If they are same, we can write only one denominator and add the numerators.

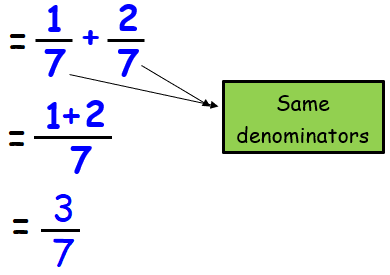
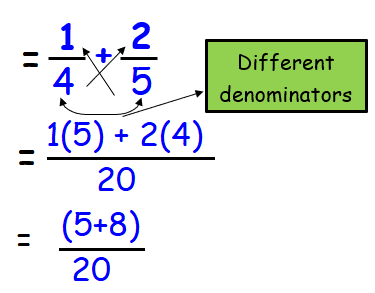
If the denominators are different, we can take least common multiple and add the fractions.

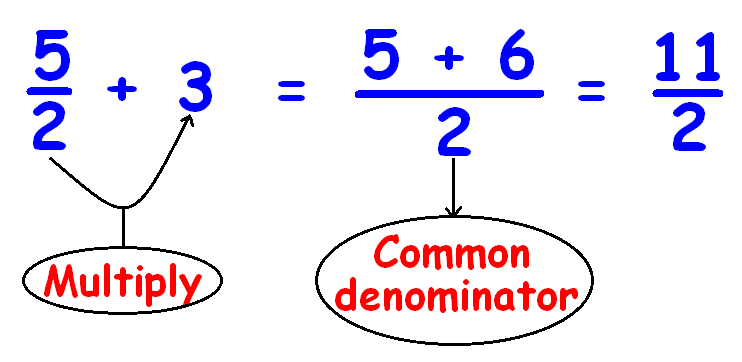
Adding fraction and integer.

Problem 1 :

(x + 1)/3 + 2

Solution :

Given, (x + 1)/3 + 2

By cross multiplication, we get

= (x + 1)/3 + 2/1

= [(x + 1) + 2 (3)] / 3

= (x + 1 + 6) / 3

= (x + 7)/3

Problem 2 :

3 + (x – 1)/4

Solution :

Given, 3 + (x – 1)/4

By cross multiplication, we get

= [3(4) + (x - 1)] / 4

= (12 + x - 1) / 4

= (11 + x)/4

Problem 3 :

(2x + 1)/6 + 2

Solution :

Given, (2x + 1)/6 + 2

By cross multiplication, we get

= [(2x + 1) + 2(6)]/6

= (2x + 1 + 12)/6

= (2x + 13) / 6

Problem 4 :

(2x + 3)/4 + (x – 1)/5

Solution :

Given, (2x + 3)/4 + (x – 1)/5

Taking the least common multiple, 

= [5(2x + 3) + 4(x - 1)]/20

= [10x + 15 + 4x - 4]/20

= (14x + 11)/20

Problem 5 :

(3x + 2)/4 + (2x + 1)/2

Solution :

Given, (3x + 2)/4 + (2x + 1)/2

Taking the least common multiple, 

= [(3x + 2) + 2(2x + 1)] / 4

= (3x + 2 + 4x + 2)/4

= (7x + 4)/4

Problem 6 :

(2x – 1)/3 + (2x + 5)/9

Solution :

Given, (2x – 1)/3 + (2x + 5)/9

Taking the least common multiple, 

= [3(2x - 1) + (2x + 5)]/9

= (6x - 3 + 2x + 5) / 9

= (8x + 2) / 9

Problem 7 :

(x + 1)/10 + (2x – 1)/5

Solution :

Given, (x + 1)/10 + (2x – 1)/5

Taking the least common multiple, 

= [(x + 1) + 2(2x - 1)] / 10

= (x + 1 + 4x - 2)/10

= (5x - 1)/10

Problem 8 :

(x – 8)/3 + (2x – 3)/5

Solution :

Given, (x – 8)/3 + (2x – 3)/5

Taking the least common multiple, 

= [5(x - 8) + 3(2x - 3)] / 15

= (5x - 40 + 6x - 9) / 15

= (11x - 49) / 15

Problem 9 :

(4x + 7)/6 + (5x – 1)/3

Solution :

Given, (4x + 7)/6 + (5x – 1)/3

Taking the least common multiple, 

= [4x + 7 + 2(5x - 1)] / 6

= (4x + 7 + 10x - 2) / 6

= (14x + 5) / 6

Problem 10 :

(1 + 3x)/7 + (2x – 3)/14

Solution :

Given, (1 + 3x)/7 + (2x – 3)/14

Taking the least common multiple, 

= [2(1 + 3x) + (2x - 3)]/14

= (2 + 6x + 2x - 3)/14

= (8x - 1)/14

Problem 11 :

w/2 - [(w + 1)/7]

Solution :

Given, w/2 - [(w + 1)/7]

Taking the least common multiple, 

= 7w/14 - [2(w + 1)/14]

= [7w - 2(w + 1)]/14

= (5w + 1)/14

Problem 12 :

2/y + 7/(y + 4)

Solution :

Given, 2/y + 7/(y + 4)

Taking the least common multiple, 

= 2/y + 7/(y + 4)

= [7(y + 4) + 7(y)]/y(y + 4)

= (7y + 28 + 4) / y² + 4y

= (7y + 32) / y² + 4y

Problem 13 :

(3x + 1)/4 + (2x - 1)/3

Solution :

Given, (3x + 1)/4 + (2x - 1)/3

Taking the least common multiple, 

= [3(3x + 1) + 4(2x - 1)]/12

= (9x + 3 + 8x - 4)/12

= (17x - 1)/12

Problem 14 :

(c - 2)/4 x [12/(2c - 4)]

Solution :

Given, (c - 2)/4 x [12/(2c - 4)]

Taking the least common multiple, 

= (c - 2)/4 x [12/2(c - 2)]

Cancelling the common factors, we get

= 6/4

= 3/2

Problem 15 :

(v + 3)/2 ÷ [(v² + 3v)/25]

Solution :

Given, (v + 3)/2 ÷ [(v² + 3v)/25]

Taking the least common multiple, 

= (v + 3)/2 x [25/(v² + 3v)]

= (v + 3)/2 x [25/v(v + 3)]

Cancelling the common factors, we get

= 25/2v

Problem 16 :

The length of the base of a triangle and its perpendicular height are:

base = (x + 5)/10 cm, height = (x - 1)/4 cm

Find an expression for the area of the triangle.

Solution :

base = (x + 5)/10 cm, height = (x - 1)/4 cm

Area of triangle = (1/2) x base x height

= (1/2) x (x + 5) /10 x (x - 1)/4

= (x + 5)(x - 1)/80 cm²

Problem 17 :

Write an expression for the area of the rectangle

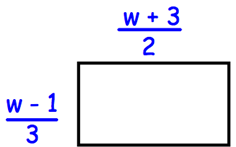
Solution :

Area of rectangle = length x width

length = (w + 3)/2 and width = (w - 1)/3

Area = (w - 1)/3 x (w + 3)/2

= (w - 1)(w + 3) / 6

= (w² + 3w - w - 3)/6

= (w² + 2w - 3)/6

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.