EXPRESSING RATIONAL NUMBERS AS DECIMALS

A rational number is any number that can be written as a ratio in the form a/b, where a and b are integers and b is not 0. Examples of rational numbers are 6 and 0.5.

7 can be written as 7/1

0.25 can be written as 1/4

Every rational number can be written as a terminating decimal or a repeating decimal. A terminating decimal, such as 0.5, has a finite number of digits.

A repeating decimal has a block of one or more digits that repeat indefinitely.

Important Points

1. Remember that the fraction bar means “divided by.” Divide the numerator by the denominator.

2. Divide until the remainder is zero or until the digits in the quotient begin to repeat.

3. Add zeros after the decimal point in the dividend as needed.  

4. When a decimal has one or more digits that repeat indefinitely, write the decimal with a bar over the repeating digit(s).

Examples

Example 1 :

Write the fraction 1/4 as a decimal. 

Solution : 

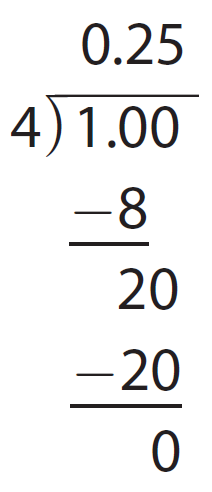
So, the decimal equal to the fraction 1/4 is 0.25

Example 2 :

Write the fraction 1/3 as a decimal. 

Solution : 

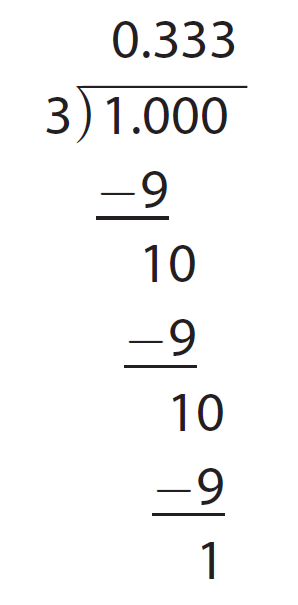
So, the decimal equal to the fraction 1/3 is 0.333......

or

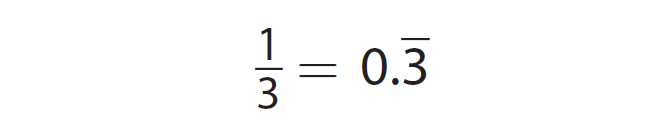
Making the Denominator as a Multiple of 10 or 100

Example 3 :

Write 96/200 as a decimal.

Solution :

Step 1 :

In the fraction 96/200, the denominator 200 is a multiple of 100.

So we can change the denominator 200 as 100 by dividing both numerator and denominator by 2.  

96/200  =  (96÷2) / (200÷2)  =  48/100

Step 2 :

In 48/100, since the denominator is 100, 48/100 can be easily converted to decimal.

In the numerator 48, there is no decimal point. Let us assume there is a decimal at the end of 48, that is (48.) 

Because we divide 48 by 100 and there are two zeros in 100, we have to move the decimal point in (48.) two digits to the left. 

So, we have 

48/100  =  0.48

Therefore, the decimal equal to the fraction 96/200 is 0.48

Example 4 :

Write 2/5 as a decimal.

Solution :

Step 1 :

In the fraction 2/5, the denominator 5 is a factor of 10. So we can change the denominator 5 as 10 by multiplying both numerator and denominator by 2.  

2/5  =  (2x2) / (5x2)  =  4/10

Step 2 :

In 4/10, since the denominator is 10, 4/10 can be easily converted to decimal.

In the numerator 4, there is no decimal point. Let us assume there is a decimal point after 4, that is (4.). 

Because we divide 4 by 10 and there is only one zero in 10, we have to move the decimal point in (4.) one digit to the left. 

So, we have 

4/10  =  0.4

Therefore, the decimal equal to the fraction 2/5 is 0.4

Example 5 :

Write 48/5 as a decimal.

Solution :

Step 1 :

In the fraction 48/5, the denominator 5 is a factor of 10. So we can change the denominator 5 as 10 by multiplying both numerator and denominator by 2.  

48/5  =  (48x2) / (5x2)  =  96/10

Step 2 :

In 96/10, since the denominator is 10, 96/10 can be easily converted to decimal.

In the numerator 96, there is no decimal point. Let us assume there is a decimal point after 96, that is (96.). 

Because we divide 96 by 10 and there is only one zero in 10, we have to move the decimal point in (96.) one digit to the left. 

So, we have 

96/10  =  9.6

Therefore, the decimal equal to the fraction 48/5 is 9.6

Example 6 :

Write 1/8 as a decimal.

Solution :

In the fraction 1/8, the denominator 8 is not a factor or multiple of 10 or 100.

And also, we can not change the denominator 8 as a multiple of 10 or 100. 

Use long division to divide the numerator by the denominator.

So, the decimal equal to the fraction 1/8 is 0.125

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.