EXTERIOR ANGLE AND REMOTE INTERIOR ANGLES OF A TRIANGLE

An interior angle of a triangle is formed by two sides of the triangle. An exterior angle is formed by one side of the triangle and the extension of an adjacent side. Each exterior angle has two remote interior angles. A remote interior angle is an interior angle that is not adjacent to the exterior angle.

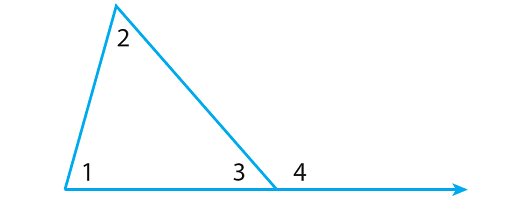
In the above diagram, 

• m∠1, m∠2, and m∠3 are interior angles.
• m∠4 is an exterior angle.
  
• m∠1 and m∠2 are remote interior angles to m∠4.
  

Relationship Between Exterior Angle and Remote Interior Angles of a Triangle

In a triangle, there is a special relationship between the measure of an exterior angle and the measures of its remote interior angles. 

Let us understand this relationship through the following steps.

Step 1 :

Sketch a triangle and label the angles as m∠1, m∠2 and m∠3.

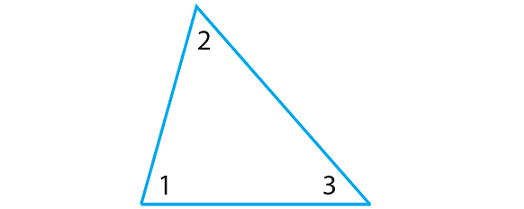
Step 2 :

According to Triangle Sum Theorem, we have

m∠1 + m∠2 + m∠3  =  180° ------ (1)

Step 3 :

Extend the base of the triangle and label the exterior angle as m∠4.

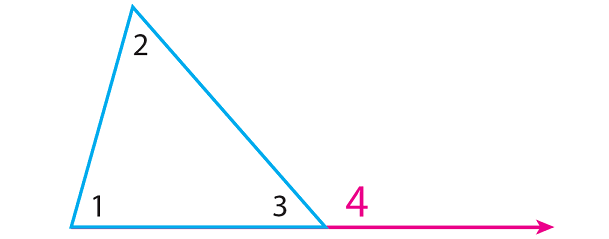
Step 4 :

m∠3 and m∠4 are the angles on a straight line. 

So, we have 

m∠3 + m∠4  =  180° ------ (2)

Step 5 :

Use the equations (1) and (2) to complete the following equation,  

m∠1 + m∠2 + m∠3  =  m∠3 + m∠4 ------ (3)

Step 6 :

Use properties of equality to simplify the equation (3). 

m∠1 + m∠2 + m∠3  =  m∠3 + m∠4

Subtract m∠3 from both sides.

m∠1 + m∠2  =  m∠4

So, the Exterior Angle Theorem states that the measure of an exterior angle of a triangle is equal to the sum of its  remote interior angles.

Reflect

Sketch a triangle and draw all of its exterior angles. 

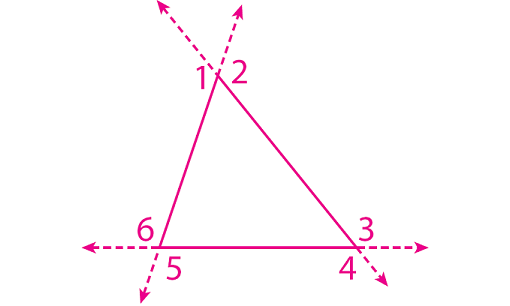
1. How many exterior angles does a triangle have at each vertex ?

2

2. How many total exterior angles does a triangle have ?

6

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.