EXTERIOR ANGLE THEOREM

This theorem is Proposition 1.16 in Euclid's Elements, which states that the measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. This is a fundamental result in absolute geometry, because its proof does not depend upon the parallel postulate.

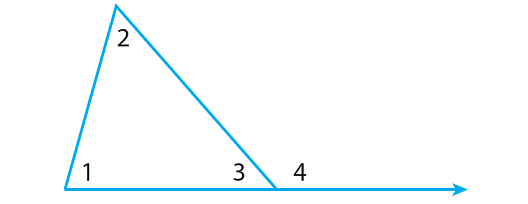
In the above diagram,

• m∠1, m∠2, and m∠3 are interior angles.
• m∠4 is an exterior angle.
  
• m∠1 and m∠2 are remote interior angles to m∠4.
  

Exterior Angle Theorem

The theorem states that the measure of an exterior  angle is equal to the sum of its  remote interior angles.

That is,

m∠1 + m∠2  =  m∠4

Proof :

There is a special relationship between the measure of an exterior angle and the measures of its remote interior angles.

Let us understand this relationship through the following steps.

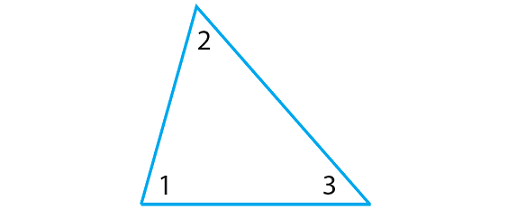
Step 1 :

Sketch a triangle and label the angles as m∠1, m∠2 and m∠3.

Step 2 :

According to Triangle Sum Theorem, we have

m∠1 + m∠2 + m∠3  =  180° ----(1)

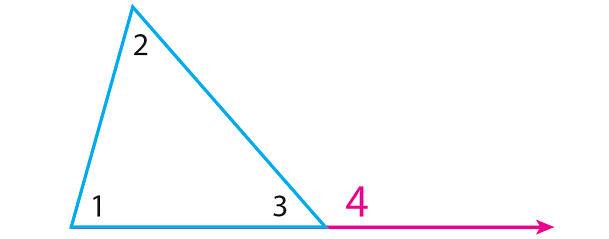
Step 3 :

Extend the base of the triangle and label the exterior angle as m∠4.

Step 4 :

m∠3 and m∠4 are the angles on a straight line.

So, we have

m∠3 + m∠4  =  180° ----(2)

Step 5 :

Use the equations (1) and (2) to complete the following equation,

m∠1 + m∠2 + m∠3  =  m∠3 + m∠4 ----(3)

Step 6 :

Use properties of equality to simplify the equation (3).

m∠1 + m∠2 + m∠3  =  m∠3 + m∠4

Subtract m∠3 from both sides.

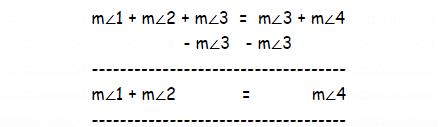
Hence, the Exterior Angle Theorem states that the measure of an exterior angle is equal to the sum of its  remote interior angles.

That is,

m∠1 + m∠2  =  m∠4

Solved Problems

Problem 1 :

Find m∠W and m∠X in the triangle given below.

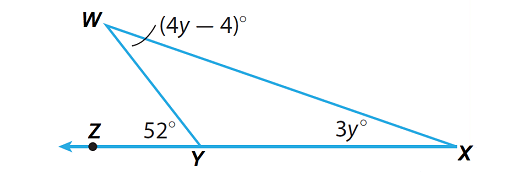
Solution :

Step 1 : 

Write the Exterior Angle Theorem as it applies to this triangle.

m∠W + m∠X  =  m∠WYZ

Step 2 : 

Substitute the given angle measures.

(4y - 4)° + 3y°  =  52°

Step 3 : 

Solve the equation for y.

(4y - 4)° + 3y°  =  52°

4y - 4 + 3y  =  52

Combine the like terms. 

7y - 4  =  52

Add 4 to both sides.

7y - 4 + 4  =  52 + 4

Simplify.

7y  =  56

Divide both sides by 7. 

7y / 7  =  56 / 7

y  =  8

Step 4 : 

Use the value of y to find m∠W and m∠X.

So, m∠W  =  28° and m∠X  =  24°.

Problem 2 :

Find m∠A and m∠B in the triangle given below.

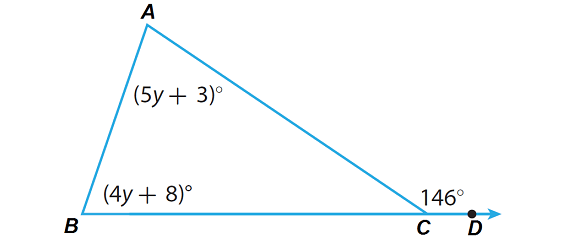
Solution :

Step 1 : 

Write the Exterior Angle Theorem as it applies to this triangle.

m∠A + m∠B  =  m∠C

Step 2 : 

Substitute the given angle measures.

(5y + 3)° + (4y + 8)°  =  146°

Step 3 : 

Solve the equation for y.

(5y + 3)° + (4y + 8)°  =  146°

5y + 3 + 4y + 8  =  146

Combine the like terms. 

9y + 11  =  146

Subtract 11 from both sides.

9y + 11 - 11  =  146 - 11

Simplify.

9y  =  135

Divide both sides by 9. 

9y / 9  =  135 / 9

y  =  15

Step 4 : 

Use the value of y to find m∠A and m∠B.

So, m∠A  =  78° and m∠B  =  68°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.