EXTERIOR ANGLE AND REMOTE INTERIOR ANGLES WORKSHEET
Problem 1 :
Sketch a triangle and label the exterior angle and its two remote interior angles.
Problem 2 :
Find the relationship between the measure of an exterior angle and the measures of its remote interior angles.
Problem 3 :
How many exterior angles does a triangle have at each vertex?
Problem 4 :
How many total exterior angles does a triangle have?

Answers
1. Answer :
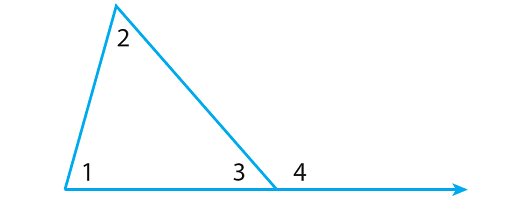
In the above diagram,
- m∠1, m∠2, and m∠3 are interior angles.
- m∠4 is an exterior angle.
- m∠1 and m∠2 are remote interior angles to m∠4.
2. Answer :
There is a special relationship between the measure of an exterior angle and the measures of its remote interior angles.
Let us understand this relationship through the following steps.
Step 1 :
Sketch a triangle and label the angles as m∠1, m∠2 and m∠3.
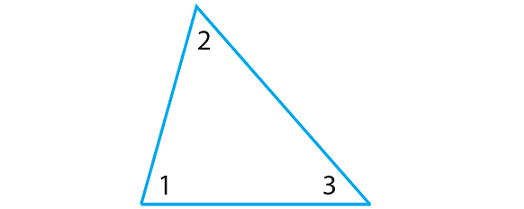
Step 2 :
According to Triangle Sum Theorem, we have
m∠1 + m∠2 + m∠3 = 180° ------ (1)
Step 3 :
Extend the base of the triangle and label the exterior angle as m∠4.
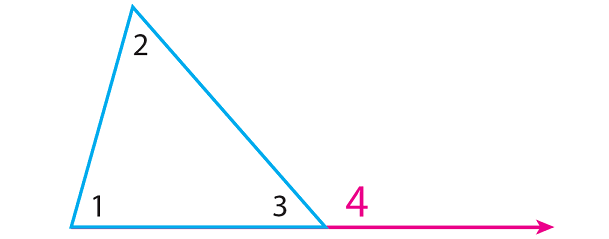
Step 4 :
m∠3 and m∠4 are the angles on a straight line.
So, we have
m∠3 + m∠4 = 180° ------ (2)
Step 5 :
Use the equations (1) and (2) to complete the following equation,
m∠1 + m∠2 + m∠3 = m∠3 + m∠4 ------ (3)
Step 6 :
Use properties of equality to simplify the equation (3).
m∠1 + m∠2 + m∠3 = m∠3 + m∠4
Subtract m∠3 from both sides.
m∠1 + m∠2 = m∠4
So, the Exterior Angle Theorem states that the measure of an exterior angle is equal to the sum of its remote interior angles.
3. Answer :
Sketch a triangle and draw all of its exterior angles.
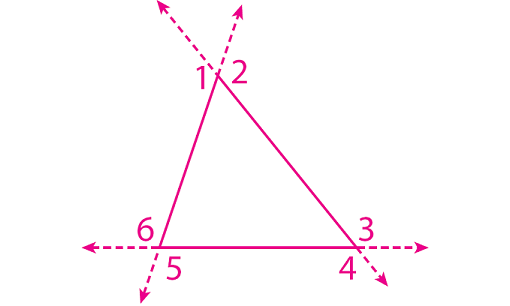
From the diagram given above, it is clear that each vertex has two exterior angles.
4. Answer :
From the diagram given in the problem 3 above, it is clear that a triangle has a total of six exterior angles.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145) -
Digital SAT Math Problems and Solutions (Part - 144)
Apr 14, 25 07:27 PM
Digital SAT Math Problems and Solutions (Part - 144)

