EXTERIOR ANGLES ON THE SAME SIDE OF THE TRANSVERSAL THEOREM

Theorem :

If two parallel lines are cut by a transversal, then exterior angles on the same side of the transversal are supplementary.

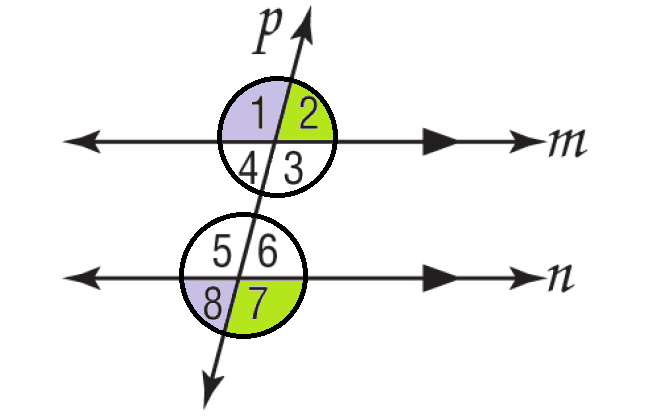
Given : m||n, p is transversal. 

Prove : ∠1 and ∠8 are supplementary and ∠2 and ∠7 are supplementary. 

Consecutive Exterior Angles :

If two lines are cut by a transversal, the pair of angles on the same side of the transversal and outside the two lines are called consecutive exterior angles. 

Exterior Angles on the Same Side of the Transversal Theorem – Converse

When two lines are cut by a transversal, if exterior angles on the same side of the transversal add up to 180°, then the two lines are parallel

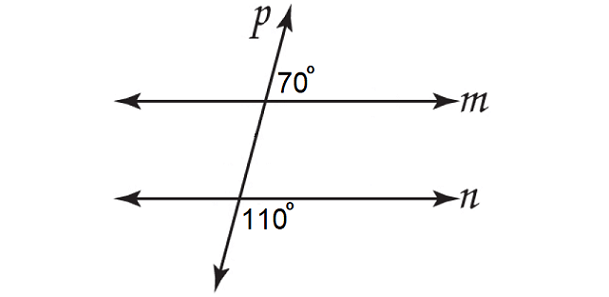
In the figure above, lines m and n are parallel. Because, a pair of angles on the same side of the transversal p and outside the two lines m and n are supplementary. 

110° + 70°  =  180°

Solved Problems

Problem 1 :

In the figure shown below, m∠1 = 105°. Find the measure of ∠8.

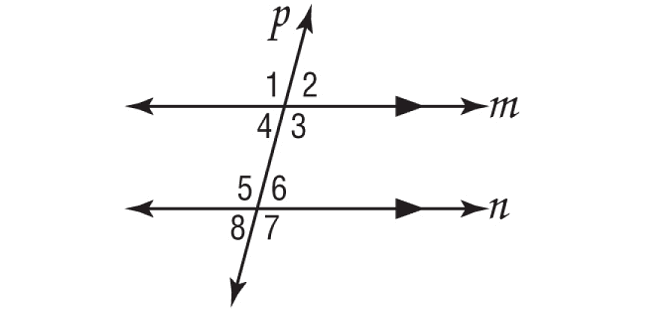
Solution :

In the figure above, lines m and n are parallel and p is transversal.

∠1 and ∠8 are on the same side of the transversal p and outside the parallel lines m and n. 

m∠1 + m∠8  =  180°

Substitute m∠1 = 105°. 

105° + m∠8  =  180°

Subtract 105° from each side. 

m∠8  =  75°

Problem 2 :

In the figure shown below, m∠1 = 102°. Find the measures ∠8, ∠15 and ∠10.

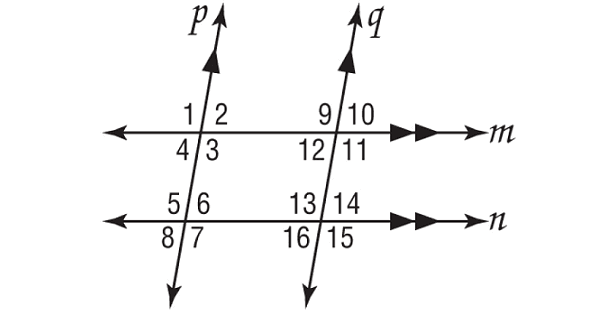
Solution :

In the figure above, lines m and n are parallel, p and q are parallel.

∠1 and ∠8 are on the same side of the transversal p and outside the parallel lines m and n. 

m∠1 + m∠8  =  180°

Substitute m∠1 = 102°. 

102° + m∠8  =  180°

Subtract 102° from each side. 

m∠8  =  78°

∠1 and ∠10 are on the same side of the transversal m and outside the parallel lines p and q. 

∠1 and ∠10 are consecutive exterior angles.

m∠1 + m∠10  =  180°

Substitute m∠1 = 102°. 

102° + m∠10  =  180°

Subtract 102° from each side. 

m∠10  =  78°

∠10 and ∠15 are on the same side of the transversal q and outside the parallel lines m and n. 

m∠10 + m∠15  =  180°

Substitute m∠10 = 78°. 

78° + m∠15  =  180°

Subtract 78° from each side. 

m∠15  =  102°

Therefore, 

m∠8  =  78°

m∠10  =  78°

m∠15  =  102°

Problem 3 :

In the figure shown below, lines m and n are parallel and p is transversal. Find the value of x. 

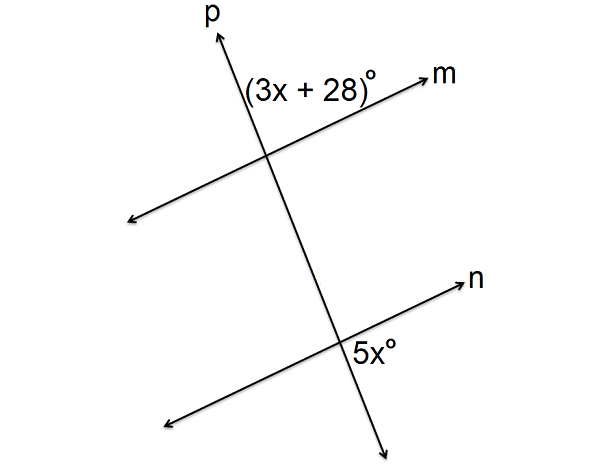
Solution :

In the figure shown above, (3x + 28)° and 5x° are on the same side of the transversal p and outside the parallel lines m and n. 

(3x + 28)° + 5x°  =  180°

3x + 28 + 5x  =  180

8x + 28  =  180

Subtract 28 from each side. 

8x  =  152

Divide each side by 8.

x  =  19

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.