FACES EDGES AND VERTICES

Observe the following shape. 

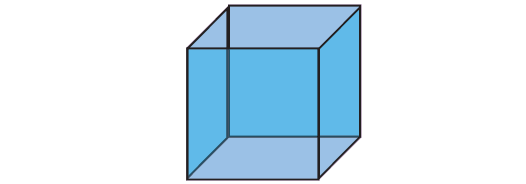
What is it?

A cube. A cube is made of six square shaped planes. These 6 square shaped planes of the cube are known as its faces.

A line segment which connects any two faces of a cube is called as Edge and each corner point where three edges meet is called as Vertex. So, a cube has 6 faces, 12 edges and 8 vertices.

Name and write the number of faces (F), vertices (V) and edges (E) for the following polyhedrons. Also find F + V – E.

Example 1 :

Solution :

Name : Cube

Face : 6

Vertices : 8

Edges : 12

F + V - E = 6 + 8 - 12 = 2

Example 2 :

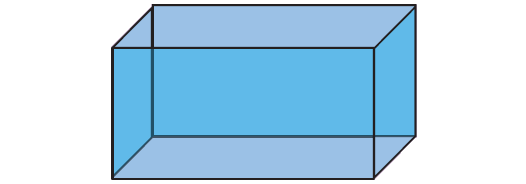
Solution :

Name : Cuboid

Face : 6

Vertices : 8

Edges : 12

F + V - E = 6 + 8 - 12 = 2

Example 3 :

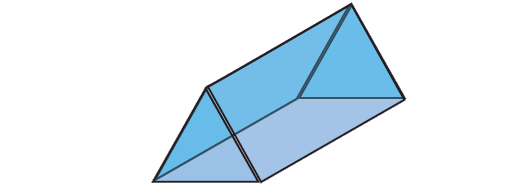
Solution :

Name : Triangular Prism

Face : 5

Vertices : 6

Edges : 9

F + V - E = 5 + 6 - 9 = 2

Example 4 :

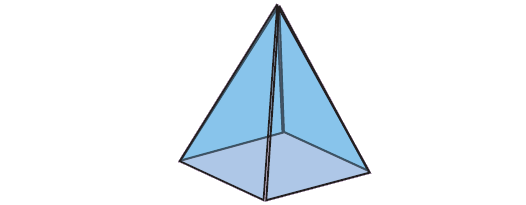
Solution :

Name : Square Pyramid

Face : 5

Vertices : 5

Edges : 8

F + V - E = 5 + 5 - 8 = 2

Example 5 :

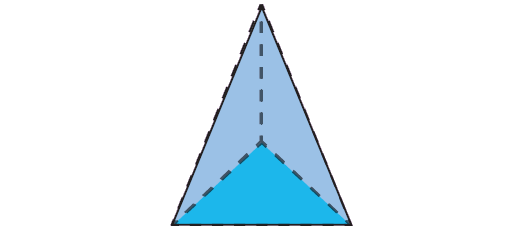
Solution :

Name : Triangular Pyramid

Face : 4

Vertices : 4

Edges : 6

F + V - E = 4 + 4 - 6 = 2

Example 6 :

Which shape has twelve edges, eight vertices and six square faces?

a) Cube     b) Cylinder    c) Cone     d) Cuboid

Solution :

• Number of faces = 6
• Number of edges = 12
• Number of vertices = 8
• The required shape is a) Cube.

Example 7 :

What is the name of a shape that has four triangular faces and one square face?

a) Square pyramid            b) Triangular pyramid

c) Triangular prism           d) Rectangular prism

Solution :

This is the most common name for the shape, which has a square base and four triangular faces meeting at the apex.

Answer: a) Square pyramid

Example 8 :

What is the name of a shape that has two triangular faces and three rectangular faces?

a) Square pyramid       b) Triangular pyramid

c) Triangular prism      d) Rectangular prism

Solution :

Number of rectangular faces = 3

Number of triangular faces = 2

Triangular face will be the base and rectangular faces will be around the figure. Then the shape must be a triangular prism

Example 9 :

What is the name of a shape that has 4 faces, 6 edges, and 4 vertices?

a) Square pyramid             b) Triangular pyramid

c) Triangular prism            d) Rectangular prism

Solution :

Number of faces = 4

Number of edges = 6

Number of vertices = 4

In square pyramid, we have 5 vertices.

In triangular prism, we have 6 vertices.

In rectangular prism, we have 8 vertices.

In triangular pyramid, we have 4 vertices, three sides would be in the shape of triangle so three faces and bottom will be square face. Totally we have 4 faces.

Answer: b) Triangular pyramid

Example 10 :

Match each shape card with an attribute that describes it.

Solution :

• Triangle will have three straight sides
• Trapezoid will have 4 vertices
• Circle will have curve paths. 0 straight sides.

Example 11 :

Find the following.

a)   surfaces     b)  vertices      c)  edges

Solution :

a)  Number of surfaces = 6

b)  Number of vertices = 8

c)  Number of edges = 12

Example 12 :

Find the following.

a)   surfaces     b)  vertices      c)  edges

Solution :

a)  Number of surfaces = 3

b)  Number of vertices = 0

c)  Number of edges = 2

Example 13 :

Find the following.

a)   surfaces     b)  vertices      c)  edges

Solution :

a)  Number of surfaces = 0

b)  Number of vertices = 0

c)  Number of edges = 0

Example 14 :

Choose the attributes of the shape.

Cylinder

a) 2 flat surfaces

b) 0 vertices

c) slides

d) two-dimensional

Solution :

In cylinder, at the top and bottom we will have 2 flat faces.

In cylinder, since there is curve path it doesn't have any vertices.

Shapes that have at least one flat face can slide, including cubes, cuboids, prisms, pyramids, and cones. These shapes can move along a flat surface without rolling, as their flat faces allow for a smooth sliding motion

Yes, a cylinder has slides because it has two flat, circular faces. While its curved surface allows it to roll, it can slide when pushed along its flat ends. 

It is 3d shape.

So, choices a, b and c are correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.