FACTOR TREE METHOD

Expressing a given number as a product of factors that are all prime numbers is called the prime factorization of a number. For example, 36 can be written as product of factors as

36  =  1 x 36

36  =  2 x 18

36  =  3 x 12

36  =  4 x 9

36  =  6 x 6

Here, the factors of 36 can be found easily as 1, 2, 3, 4, 6, 9, 12, 18 and 36. Note that not all the factors of 36 are prime numbers. To find the prime factors of 36, we do the prime factorization by factor tree method. 

One of the ways to find the prime factorization of a number is to use a visual representation called factor tree. As we add more branches, we will see that this visual representation looks like an upside down tree.

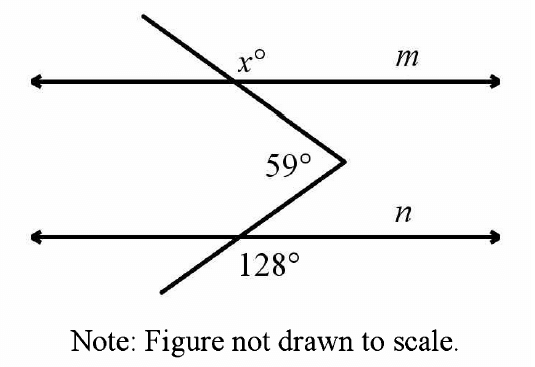
Let us find the prime factorization of 36 using factor tree as shown below.

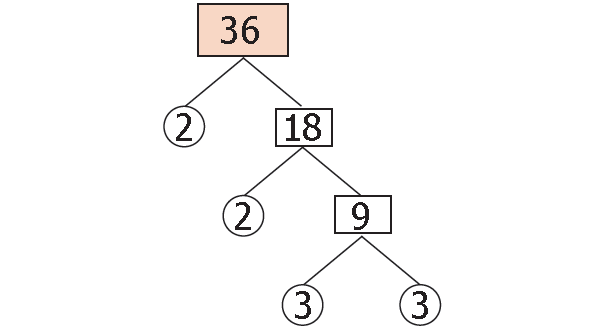
Prime factorization of 36 :

36  =  2 x 2 x 3 x 3

Key Concept

In each step put a prime factor (e.g. 2, 3, 5, 7, 11, 13, etc.) into the CIRCLE and the other factor into the BOX .

In the next step, factor the number in the BOX by putting one of its prime factors into the CIRCLE and the other factor into the BOX .

Continue until you reach a number which has only two prime factors and put each of them into a CIRCLE.

Then, write down all of the  factors in the CIRCLES and that is your prime factorization of the original number.

Examples : 

Find the prime factors  of the following numbers. 

1)  56

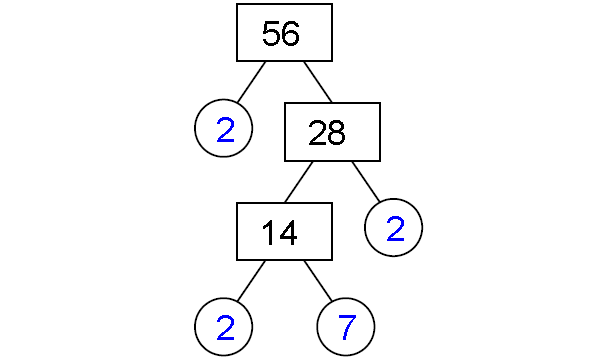
Prime factorization of 56 :

56  =  2 x 2 x 2 x 7

2)  24

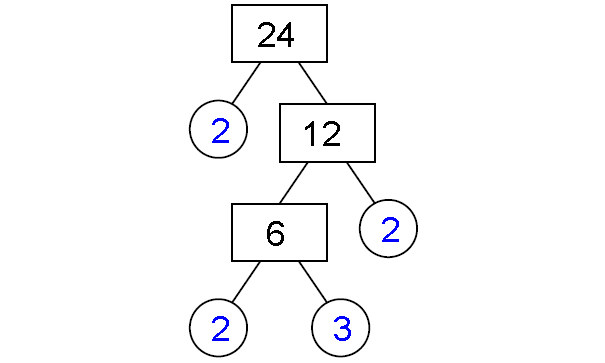
Prime factorization of 24 :

24  =  2 x 2 x 2 x 3

3)  50

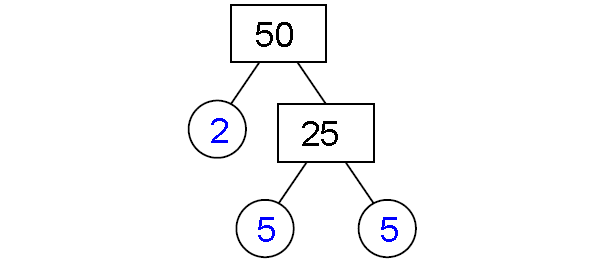
Prime factorization of 50 :

50  =  2 x 5 x 5

4)  108

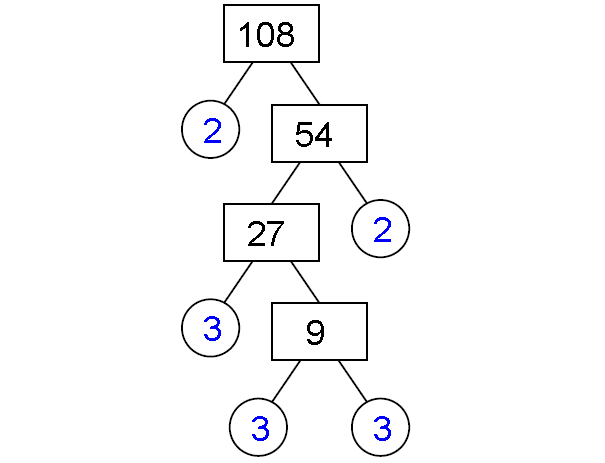
Prime factorization of 108 :

108  =  2 x 2 x 3 x 3 x 3

5)  80

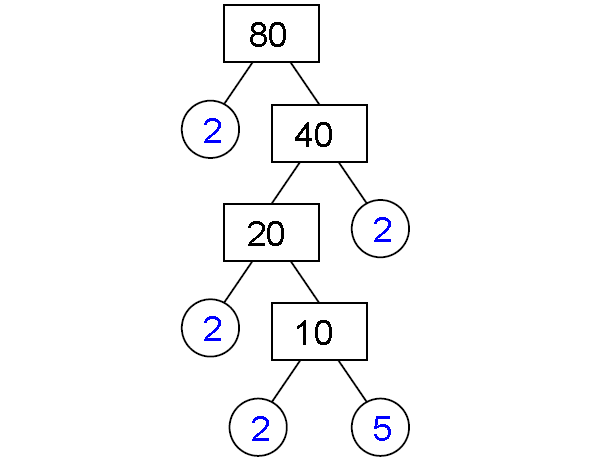
Prime factorization of 80 :

80  =  2 x 2 x 2 x 2 x 5

6)  54

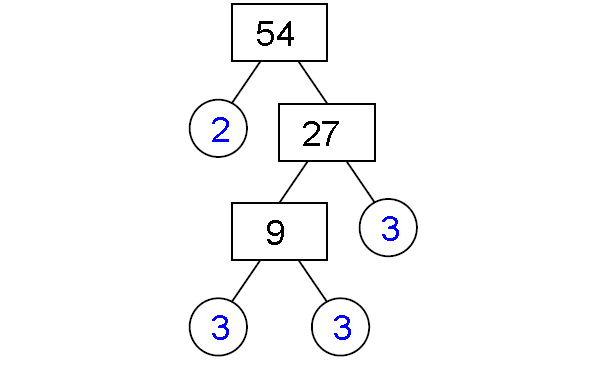
Prime factorization of 54 :

54  =  2 x 3 x 3 x 3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.