FACTORED FORM OF A QUADRATIC FUNCTION WORKSHEET
Problem 1 :
Write the following quadratic function in factored form.
f(x) = x2 - 5x + 6
Problem 2 :
Write the following quadratic function in factored form.
f(x) = 2x2 - 3x - 9
Problem 3 :
Solve the following quadratic equation by factoring :
x2 + 2x = 14
Problem 4 :
Solve the following quadratic equation by factoring :
3x2 - 14x + 8 = 0
Problem 5 :
A ball is thrown upwards from a rooftop which is above from the ground. It will reach a maximum vertical height and then fall back to the ground. The height of the ball "h" from the ground at time "t" seconds is given by, h = -16t2 + 64t + 80. How long will the ball take to hit the ground ?
Problem 6 :
Identify the intervals on which the quadratic function
y = x2 - 2x - 3
is positive and negative.
Problem 7 :
Write the equation of a parabola with x-intercepts
(-3, 0) and (2, 0)
and which passes through the point (3, 30).
Problem 8 :
The graph shows the function defined by y = x2 + 2x - 8. How do the zeros of the function relate to the factors of the expression x2 + 2x - 8 ?

Detailed Answer Key
Problem 1 :
Write the following quadratic function in factored form.
f(x) = x2 - 5x + 6
Solution :
Step 1 :
Multiply the coefficient of x2, 1 by the constant term 14.
1 x 6 = 6
Step 2 :
Factor 6 into two parts such that sum of the two parts is equal to the coefficient of x, -5 and the product is equal to 6.
Then, we have
6 = (-2)(-3)
Step 3 :
Using (-2) and (-3), factor the given quadratic expression.
x2 - 5x + 6 = x2 - 2x - 3x + 6
x2 - 5x + 6 = x(x - 2) - 3(x - 2)
x2 - 5x + 6 = (x - 2)(x - 3)
Therefore, the factored form of the given quadratic function is
f(x) = (x - 2)(x - 3)
Problem 2 :
Write the following quadratic function in factored form.
f(x) = 2x2 - 3x - 9
Solution :
Step 1 :
Multiply the coefficient of x2, 2 by the constant term -9.
2 x (-9) = -18
Step 2 :
Factor -18 into two parts such that sum of the two parts is equal to the coefficient of x, -3 and the product is equal to -18.
Then, we have
-18 = (+3)(-6)
Step 3 :
Using (+3) and (-6), factor the given quadratic expression.
2x2 - 3x - 9 = 2x2 + 3x - 6x - 9
2x2 - 3x - 9 = x(2x + 3) - 3(2x + 3)
2x2 - 3x - 9 = (2x + 3)(x - 3)
Therefore, the factored form of the given quadratic function is
f(x) = (2x + 3)(x - 3)
Problem 3 :
Solve the following quadratic equation by factoring :
x2 + 2x = 14
Solution :
Write the above equation in the form
ax2 + bx +c = 0
Then,
x2 + 2x - 14 = 0
Factor.
(x + 7)(x - 2) = 0
(x + 7) = 0 or (x - 2) = 0
x = - 7 or x = 2
Problem 4 :
Solve the following quadratic equation by factoring :
3x2 - 14x + 8 = 0
Solution :
3x2 - 14x + 8 = 0
Factor.
3x2 - 2x - 12x + 8 = 0
x(3x - 2) - 4(3x - 2) = 0
3x - 2 = 0 or (x - 4) = 0
x = 2 / 3 or x = 4
Problem 5 :
A ball is thrown upwards from a rooftop which is above from the ground. It will reach a maximum vertical height and then fall back to the ground. The height of the ball "h" from the ground at time "t" seconds is given by, h = -16t2 + 64t + 80.How long will the ball take to hit the ground ?
Solution :
When the ball hits the ground, height "h" = 0.
So, we have
0 = -16t2 + 64t + 80
16t2 - 64t - 80 = 0
Divide each side by 16.
t2 - 4t - 5 = 0
(t - 5)(t + 1) = 0
t = 5 or t = - 1
t = - 1 can not be accepted. Because time can never be a negative value.
Hence, the ball will take 5 seconds to hit the ground.
Problem 6 :
Identify the intervals on which the quadratic function
y = x2 - 2x - 3
is positive and negative.
Solution :
The y-values of quadratic function will either turn from positive to negative or from negative to positive, when the graph crosses the x-axis.
Find the zeros of the function to identify these points.
To find zeros, set the quadratic expression x2 - 2x - 3 equal to 0.
x2 - 2x - 3 = 0
Factor.
(x - 3)(x + 1) = 0
By Zero Product Property,
(x - 3) = 0 or (x + 1) = 0
Solve.
x = 3 or x = -1
Two zeros create three intervals. Choose an x-value to test each interval. Substitute the x-value into the original expression to determine, if the corresponding y-value is positive or negative.
x < -1
Choose x = -3
y = (-3)²- 2(-3) - 3
y = 9 + 6 - 3
y = 12
Positive
-1 < x < 3
Choose x = 1
y = (1)²- 2(1) - 3
y = 1 - 2 - 3
y = - 4
Negative
x < -1
Choose x = 6
y = (6)²- 2(6) - 3
y = 36 - 12 - 3
y = 21
Positive
Graph the function to verify where the function is positive or negative.
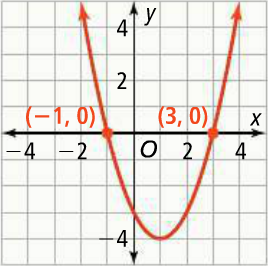
The function is positive when the graph is above the x-axis, or on the intervals
x < -1 and x > 3
The function is negative when the graph is below the x-axis, or on the interval
-1 < x < 3
Problem 7 :
Write the equation of a parabola with x-intercepts
(-3, 0) and (2, 0)
and which passes through the point (3, 30).
Solution :
Write the general form of a factored quadratic equation.
y = a(x - p)(x - q)
Substitute -2 and 5 for zeros.
y = a[x - (-3)][x - 2]
Simplify.
y = a(x + 3)(x - 2) -----(1)
Substitute 3 for x and 30 for y.
30 = a(3 + 3)(3 - 2)
Simplify.
30 = a(6)(1)
30 = 6a
Divide each side.
5 = a
Substitute 5 for a in (1).
y = 5(x + 3)(x - 2)
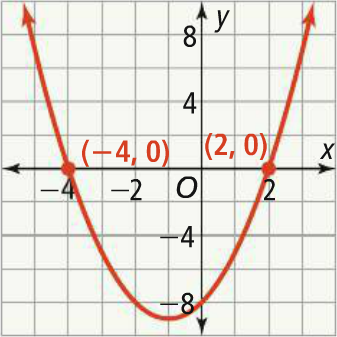
Problem 8 :
The graph shows the function defined by y = x2 + 2x - 8. How do the zeros of the function relate to the factors of the expression x2 + 2x - 8 ?

Solution :
The expression x2 + 2x - 8 can be expressed as a product of two factors.
The factors of -8 have a sum of 2 are -2 and 4.
That is,
y = x2 + 2x - 8 -----> y = (x - 2)(x + 4)
The x-intercepts of the graph are -4 and 2. So the zeros of the function are x = -4 and x = 2.
Substitute x = -4 and x = 2 into the factored form of the equation.
y = (-4 - 2)(-4 + 4) -----> y = (-6)(0) = 0
y = (2 - 2)(2 + 4) -----> y = (0)(6) = 0
The factors, (x + 4) and (x - 2), are related to the zeros
x = - 4 and x = 2
Because each of the zeros make one of the factors 0.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 146)
Apr 18, 25 06:52 AM
Digital SAT Math Problems and Solutions (Part - 146) -
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145)

