FACTORED FORM OF A QUADRATIC FUNCTION

The factored form of a quadratic function is 

f(x)  =  a(x - p)(x - q)

where p and q are the zeros of f(x).

Factoring Quadratic Functions

Example 1 : 

Write the following quadratic function in factored form. 

f(x)  =  x² - 5x + 6

Solution :

Step 1 :

Multiply the coefficient of x², 1 by the constant term 14. 

1 ⋅ 6  =  6

Step 2 :

Factor 6 into two parts such that sum of the two parts is equal to the coefficient of x, -5 and the product is equal to 6.

Then, we have

6  =  (-2)(-3)

Step 3 : 

Using (-2) and (-3), factor the given quadratic expression. 

x² - 5x + 6  =  x² - 2x - 3x + 6

x² - 5x + 6  =  x(x - 2) - 3(x - 2)

x² - 5x + 6  =  (x - 2)(x - 3)

Therefore, the factored form of the given quadratic function is 

f(x)  =  (x - 2)(x - 3)

Example 2 : 

Write the following quadratic function in factored form. 

f(x)  =  2x² - 3x - 9

Solution :

Step 1 :

Multiply the coefficient of x², 2 by the constant term -9. 

2 x (-9)  =  -18

Step 2 :

Factor -18 into two parts such that sum of the two parts is equal to the coefficient of x, -3 and the product is equal to -18.

Then, we have

-18  =  (+3)(-6)

Step 3 : 

Using (+3) and (-6), factor the given quadratic expression. 

2x² - 3x - 9  =  2x² + 3x - 6x - 9

2x² - 3x - 9  =  x(2x + 3) - 3(2x + 3)

2x² - 3x - 9  =  (2x + 3)(x - 3)

Therefore, the factored form of the given quadratic function is 

f(x)  =  (2x + 3)(x - 3)

Relate Factors to Zeros of a Function

Example :

The graph shows the function defined by y  =  x² + 2x - 8. How do the zeros of the function relate to the factors of the expression x² + 2x - 8 ?

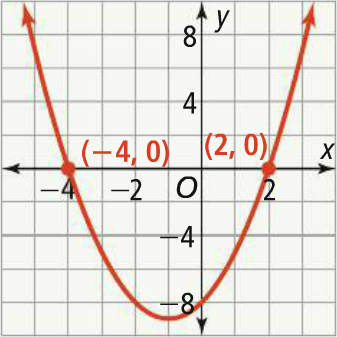
Solution : 

The expression x² + 2x - 8 can be expressed as a product of two factors. 

The factors of -8 have a sum of 2 are -2 and 4. 

That is, 

y  =  x² + 2x - 8 -----> y  =  (x - 2)(x + 4)

The x-intercepts of the graph are -4 and 2. So the zeros of the function are x = -4 and x = 2.

Substitute x  =  -4 and x  =  2 into the factored form of the equation. 

y  =  (-4 - 2)(-4 + 4) -----> y  =  (-6)(0)  =  0

y  =  (2 - 2)(2 + 4) -----> y  =  (0)(6)  =  0

The factors, (x + 4) and (x - 2), are related to the zeros 

x  =  - 4 and x  =  2

Because each of the zeros make one of the factors 0.

Zero Product Property

The Zero Product Property states that if a product of real-number factors is 0, then at least one of the factors must be 0.

In the case of two factors, if pq  =  0, then either 

p  =  0  or  q  =  0, or both

To use the Zero Product Property, rewrite the equation, so that it is an expression equals to 0, then factor and solve.  

Solve Quadratic Equations by Factoring

Example 1 :

Solve the following quadratic equation by factoring :

x² + 2x  =  14

Solution :

Write the above equation in the form 

ax² + bx +c  =  0

Then, 

x² + 2x - 14  =  0

Factor. 

(x + 7)(x - 2)  =  0

(x + 7)  =  0  or  (x - 2)  =  0

x  =  - 7  or  x  =  2

Example 2 :

Solve the following quadratic equation by factoring :

3x² - 14x + 8  =  0

Solution :

3x² - 14x + 8  =  0

Factor.

3x² - 2x - 12x + 8  =  0

x(3x - 2) - 4(3x - 2)  =  0

3x - 2  =  0  or  (x - 4)  =  0

x  =  2 / 3  or  x  =  4

Find the Zeros of a Quadratic Function

Example : 

A ball is thrown upwards from a rooftop which is above from the ground. It will reach a maximum vertical height and then fall back to the ground. The height of the ball "h" from the ground at time "t" seconds is given by, h = -16t² + 64t + 80.How long will the ball take to hit the ground?

Solution :

When the ball hits the ground, height "h"  =  0.

So, we have  

0  =  -16t² + 64t + 80

16t² - 64t - 80  =  0

Divide each side by 16.

t² - 4t - 5  =  0

(t - 5)(t + 1)  =  0

t  =  5  or  t  =  - 1

t  =  - 1 can not be accepted. Because time can never be a negative value. 

Hence, the ball will take 5 seconds to hit the ground.

Determine Positive and Negative Intervals

Example :

Identify the intervals on which the quadratic function

y  =  x² - 2x - 3

is positive and negative. 

Solution :

The y-values of quadratic function will either turn from positive to negative or from negative to positive, when the graph crosses the x-axis. 

Find the zeros of the function to identify these points. 

To find zeros, set the quadratic expression x² - 2x - 3 equal to 0.

x² - 2x - 3  =  0

Factor.

(x - 3)(x + 1)  =  0

By Zero Product Property, 

(x - 3)  =  0  or  (x + 1)  =  0

Solve.

x  =  3  or  x  =  -1

Two zeros create three intervals. Choose an x-value to test each interval. Substitute the x-value into the original expression to determine, if the corresponding y-value is positive or negative.   

Graph the function to verify where the function is positive or negative. 

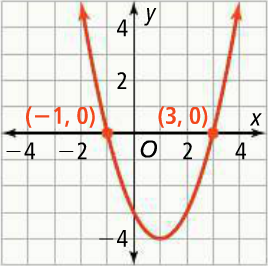
The function is positive when the graph is above the x-axis, or on the intervals

x < -1 and x > 3

The function is negative when the graph is below the x-axis, or on the interval

-1 < x < 3

Write the Equation of a Parabola in Factored Form 

Example :

Write the equation of a parabola with x-intercepts 

(-3, 0) and (2, 0)

and which passes through the point (3, 30)

Solution : 

Write the general form of a factored quadratic equation. 

y  =  a(x - p)(x - q)

Substitute -2 and 5 for zeros. 

y  =  a[x - (-3)][x - 2]

Simplify.

y  =  a(x + 3)(x - 2) -----(1)

Substitute 3 for x and 30 for y.

30  =  a(3 + 3)(3 - 2)

Simplify.

30  =  a(6)(1)

30  =  6a

Divide each side.

5  =  a

Substitute 5 for a in (1).

y  =  5(x + 3)(x - 2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.