FACTORING 4TH DEGREE POLYNOMIALS

Example 1 :

Factor the following polynomial given that the product of two of the zeros is 8.

x⁴ + 2x³ - 25x² - 26x + 120 

Solution :

Because the product two of the zeros is 8, we can try 2 and 4 in synthetic division.

x = 2 and x = 4 are the two zeros of the given polynomial of degree 4.

Because x = 2 and x = 4 are the two zeros of the given polynomial, the two factors are (x - 2) and (x - 4). 

To find other factors, factor the quadratic expression which has the coefficients 1, 8 and 15.

That is, x² + 8x + 15.

x² + 8x + 15  =  (x + 3)(x + 5)

So, the factors of the given polynomial are 

(x - 2), (x - 4), (x + 3) and (x + 5)

Example 2 :

Factor : 

x⁴ - 10x³ + 37x² - 60x + 36

Solution :

By trial and error, we can check whether 1 is a zero of the above polynomial. 

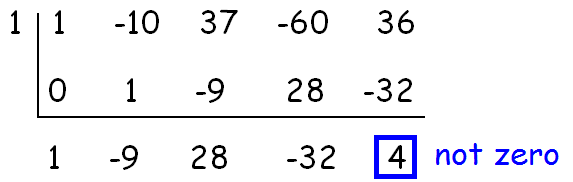
Because the remainder is 4 (not zero), 1 is not a zero of the given polynomial.

Now, let us check with -1.

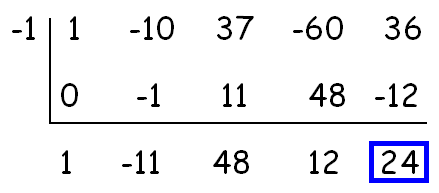
Because the remainder is 24 (not zero), -1 is not a zero of the given polynomial.

Now, let us check with 2. 

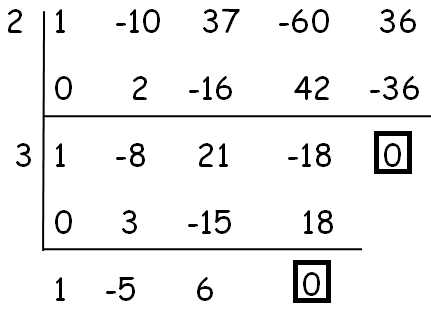
Both x = 2 and x = 3 are the two zeros of the given polynomial.

Because x = 2 and x = 3 are the two zeros of the given polynomial, the two factors are (x - 2) and (x - 3). 

To find other factors, factor the quadratic expression which has the coefficients 1, -5 and 6.

That is, x² - 5x + 6.

x² - 5x + 6  =  (x - 2)(x - 3)

So, the factors of the given polynomial are 

(x - 2), (x - 3), (x - 2) and (x - 3)

Example 3 :

x⁴ - 2x² - 15

Solution :

= x⁴ - 2x² - 15

Let x² = t

= (x²)² - 2x² - 15

= t² - 2t - 15

Now it is in the form of quadratic polynomial or trinomial.

= t² - 5t + 3t - 15

= t(t - 5) + 3(t - 5)

= (t + 3)(t - 5)

Applying the value of t, we get

= (x² + 3)(x² - 5)

So, the factors are (x² + 3)(x² - 5)

Example 4 :

x⁴ + 14x² + 45

Solution :

= x⁴ + 14x² + 45

Let x² = t

= (x²)² + 14x² + 45

= t² + 14t + 45

Now it is in the form of quadratic polynomial or trinomial.

= t² + 9t + 5t + 45

= t(t + 9) + 5(t + 9)

= (t + 9)(t + 5)

Applying the value of t, we get

= (x² + 9)(x² + 5)

So, the factors are (x² + 9)(x² + 5).

Example 5 :

x⁴ - 13x² + 40

Solution :

= x⁴ - 13x² + 40

Let x² = t

= (x²)² - 13x² + 40

= t² - 13t + 40

Now it is in the form of quadratic polynomial or trinomial.

= t² - 8t - 5t + 40

= t(t - 8) - 5(t - 8)

= (t - 8)(t - 5)

Applying the value of t, we get

= (x² - 8)(x² - 5)

So, the factors are (x² - 8)(x² - 5).

Example 6 :

8 x⁴ + 10 x² − 3

Solution :

= 8 x⁴ + 10 x² − 3

Let x² = t

= 8(x²)² + 10x² - 3

= 8t² + 10t - 3

Now it is in the form of quadratic polynomial or trinomial.

= 8t² + 12t - 2t - 3

= 4t(2t + 3) - (2t + 3)

= (4t - 1)(2t + 3)

So, the factors are (4t - 1)(2t + 3).

Example 7 :

f(x) = x⁴ + 2x³ − x² − 2x

Solution :

f(x) = x⁴ + 2x³ − x² − 2x

= x(x³ + 2x² − x - 2)

Factoring x² from the first two terms and factoring negative sign from last two terms.

= x[x² (x + 2) − (x - 2)]

= x(x² - 1)(x + 2)

= x(x² - 1²)(x + 2)

= x(x + 1)(x - 1)(x + 2)

So, the factors are x(x + 1)(x - 1)(x + 2).

Example 8 :

Show that x + 3 is a factor of f(x) = x⁴ + 3x³ − x − 3. Then factor f(x) completely.

Solution :

f(x) = x⁴ + 3x³ − x − 3

Factor x³, we get

f(x) = x³ (x + 3) − 1(x + 3)

= (x³ - 1)(x + 3) -------(1)

a³ - b³ = (a - b) (a² + ab + b²)

x³ - 1³ = (x - 1) (x² + x(1) + 1²)

= (x - 1) (x² + x + 1)

Applying these factors, we get

= (x - 1) (x² + x + 1) (x + 3)

So, factors are (x - 1) (x² + x + 1) (x + 3).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.