FACTORING POLYNOMIALS WITH SYNTHETIC DIVISION WORKSHEET

Factor each of the following polynomials using synthetic division :

1) x³ - 3x² - 10x + 24

2) 2x³ - 3x² - 3x + 2

3)  -7x + 3 + 4x³

4)  x³ + x² - 14x - 24

5)  x³  - 7x + 6

6)  x³ - 10x² - x + 10

1. Answer :

x³ - 3x² - 10x + 24

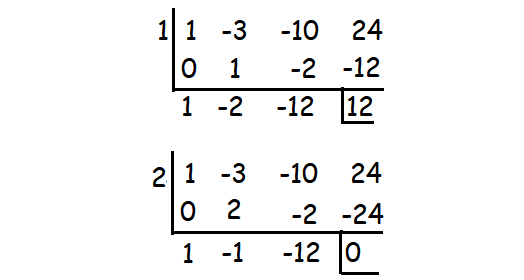
By Substituting x = 2, we get the remainder 0.

So (x - 2) is a factor.

Then, 

x² - x - 12 = x² - 4x + 3x - 12

x² - x - 12 = x(x - 4) + 3(x - 4)

x² - x - 12 = (x + 3)(x - 4)

Therefore, the factors are (x - 2)(x + 3)(x- 4).

2. Answer :

2x³ - 3x² - 3x + 2

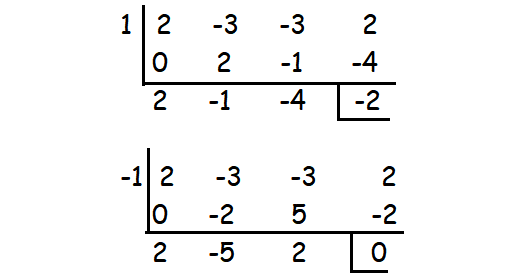
By substituting x = -1, we get the remainder 0.

So (x + 1) is a factor.

Then,

2x² - 5x + 2 = 2x² - 4x - x + 2

2x² - 5x + 2 = 2x(x - 2) - 1(x - 2)

2x² - 5x + 2 = (2x - 1)(x - 2)

Therefore, the factors are (x + 1)(2x - 1)(x - 2).

3. Answer :

-7x + 3 + 4x³

-7x + 3 + 4x³  =  4x³ + 0x² - 7x + 3

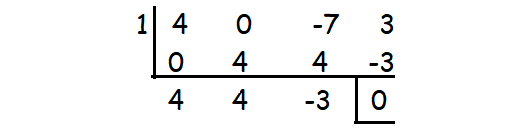
By substituting x = 1, we get the remainder 0.

So (x - 1) is a factor.

Then,

4x² + 4x - 3 = 4x² + 6x - 2x - 3

4x² + 4x - 3 = 2x(2x + 3) - 1(2x + 3)

4x² + 4x - 3 = (2x - 1)(2x + 3)

Therefore, the factors are (x - 1)(2x - 1)(2x + 3).

4. Answer :

x³ + x² - 14x - 24

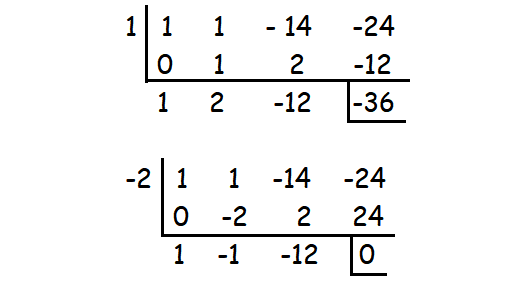
By substituting x = -2, we get the remainder 0.

So (x + 2) is a factor.

Then,

x² - x - 12 = x² - 4x  + 3x - 12

x² - x - 12 = x(x - 4) + 3(x - 4)

x² - x - 12 = (x + 3)(x - 4)

Therefore, the factors are (x + 2)(x + 3)(x - 4).

5. Answer :

x³  - 7x + 6

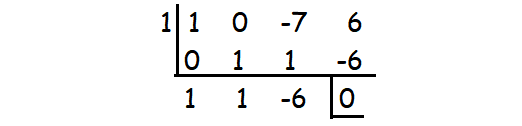
By substituting x = 1, we get the remainder 0.

So (x - 1) is a factor.

Then,

x² + x - 6 = x² + 3x  - 2x - 6

x² + x - 6 = x(x + 3) - 2(x + 3)

x² + x - 6 = (x + 3)(x - 2)

Therefore, the factors are (x - 2)(x + 3)(x - 1).

6. Answer :

x³ - 10x² - x + 10

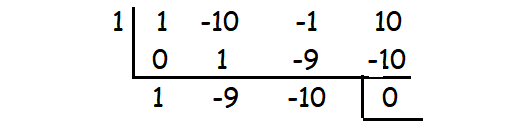
By substituting x = 1, we get the remainder 0.

So (x - 1) is a factor.

Then,

x² - 9x - 10 = x² - 10x + 1x - 10

x² - 9x - 10 = x(x - 10) + 1(x - 10)

x² - 9x - 10 = (x + 1)(x - 10)

Therefore, the factors are (x + 1)(x - 10)(x - 1).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.