FACTORING SPECIAL PRODUCTS WORKSHEET

Problems 1-4 : Determine whether each trinomial is a perfect square. If so, factor. If not, explain.

Problem 1 : 

x² + 12x + 36

Problem 2 : 

9x² + 12x + 4

Problem 3 : 

4x² - 12x + 9

Problem 4 : 

x² + 9x + 16

Problems 5-8 : Determine whether each binomial is a difference of two squares. If so, factor. If not, explain.

Problem 5 :

x² - 81

Problem 6 : 

4x² - 9

Problem 7 : 

9p⁴ - 16q²

Problem 8 : 

x⁶ - 7y²

Problems 9-12 : Factor the given trinomial.

Problem 9 : 

x² + 6x + 9

Problem 10 : 

4y² + 20y + 25

Problem 11 : 

81z² - 18z + 1

Problem 12 : 

100k² - 140k + 49

Problems 13-16 : Factor the given binomial.

Problem 13 :

x² - 144

Problem 14 :

25y² - 169

Problem 15 :

9a² - 16b²

Problem 16 :

c⁴ - d⁴

Answers

1. Answer :

x² + 12x + 36

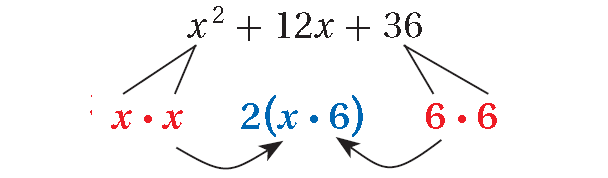
The trinomial is a perfect square. Factor.

x² + 12x + 36

a = x, b = 6.

Write the trinomial as a² + 2ab + b².

= x² + 2(x)(6) + 6²

Write the trinomial as (a + b)².

= (x + 6)²

2. Answer :

9x² + 12x + 4

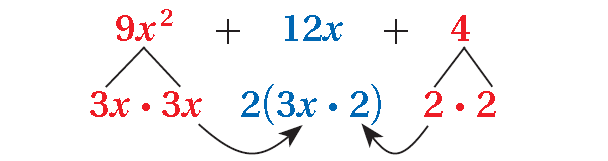
The trinomial is a perfect square. Factor.

9x² + 12x + 4

a = 3x, b = 2. 

Write the trinomial as a² + 2ab + b².

= (3x)² + 2(3x)(2) + 2²

Write the trinomial as (a + b)².

= (3x + 2)²

3. Answer :

4x² - 12x + 9

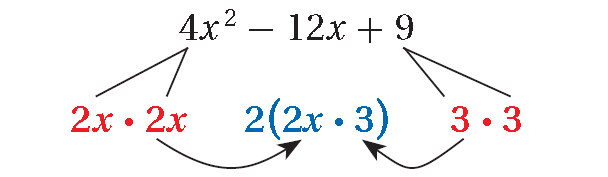
The trinomial is a perfect square. Factor.

= 4x² - 12x + 9

a = 2x, b = 3. 

Write the trinomial as a² - 2ab + b².

= (2x)² - 2(2x)(3) + 3²

Write the trinomial as (a - b)².

= (2x - 3)²

4. Answer :

x² + 9x + 16

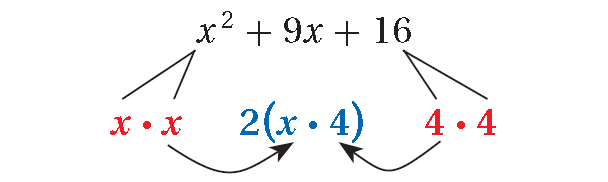
2(x · 4)  ≠  9x

x² + 9x + 16 is not a perfect-square trinomial because

9x ≠ 2(x · 4)

5. Answer :

x² - 81

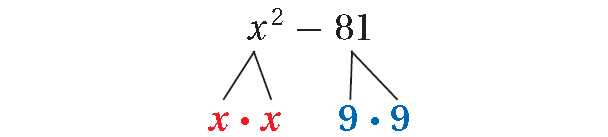
The polynomial is a difference of two squares.

= x² - 81

= x² - 9²

a = x and b = 9, write the polynomial as (a + b)(a - b).

=  (x + 9)(x - 9)

6. Answer :

4x² - 9

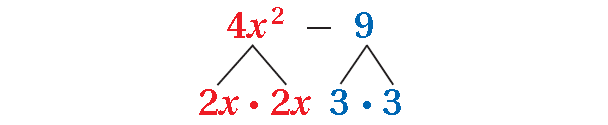
The polynomial is a difference of two squares.

= 4x² - 9

= (2x)² - 3²

a = 2x and b = 3, write the polynomial as (a + b)(a - b).

=  (2x + 3)(2x - 3)

7. Answer :

9p⁴ - 16q²

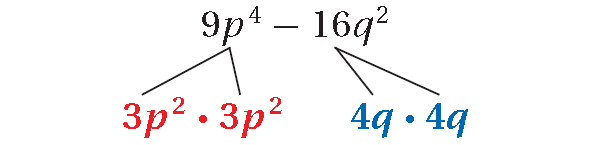
The polynomial is a difference of two squares.

= 9p⁴ - 16q²

= (3p²)² - (4q)²

a = 3p² and b = 4q, write the polynomial as (a + b)(a - b).

= (3p² + 4q)(3p² - 4q)

8. Answer :

x⁶ - 7y²

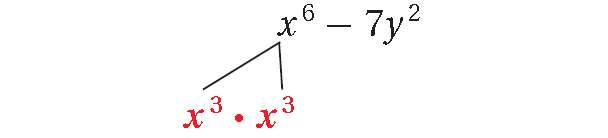
7y² is not a perfect square.

x⁶ - 7y² is not the difference of two squares because 7y² is not a perfect square.

9. Answer :

= x² + 6x + 9

= x² + 2(x)(3) + 3²

Since the above expression is in the form of a² + 2ab + b², it can be written in the form (a + b)².

= (x + 3)²

10. Answer :

= 4y² + 20y + 25

= 2²y² + 20y + 5²

= (2y)² + 2(2y)(5) + 5²

Since the above expression is in the form of a² + 2ab + b², it can be written in the form (a + b)².

= (2y + 5)²

11. Answer :

81z² - 18z + 1

= 9²z² - 18z + 1²

= 9²z² - 2(9z)(1) + 1²

= (9z)² - 2(9z)(1) + 1²

Since the above expression is in the form of a² - 2ab + b², it can be written in the form (a - b)².

= (9z - 1)²

12. Answer :

100k² - 140k + 49

= 10²k² - 140k + 7²

= (10k)² - 2(10k)(7) + 7²

Since the above expression is in the form of a² - 2ab + b², it can be written in the form (a - b)².

= (10k - 7)²

13. Answer :

= x² - 144

= x² - 12²

The above binomial is a difference of two squares and it is in the form of (a² - b²). Take a = x and b = 12 and write the above binomial in the factored form (a + b)(a - b).

= (x + 12)(x - 12)

14. Answer :

= 25y² - 169

= 5²y² - 13²

= (5y)² - 13²

The above binomial is a difference of two squares and it is in the form of (a² - b²). Take a = 5y and b = 13 and write the above binomial in the factored form (a + b)(a - b).

= (5y + 13)(5y - 13)

15. Answer :

= 9a² - 16b²

= 3²a² - 4²b²

= (3a)² - (4b)²

The above binomial is a difference of two squares and it is in the form of (a² - b²). Take a = 3a and b = 4b and write the above binomial in the factored form (a + b)(a - b).

= (3a + 4b)(3a - 4b)

16. Answer :

= c⁴ - d⁴

= (c²)² - (d²)²

= (c²)² - (d²)²

The above binomial is a difference of two squares and it is in the form of (a² - b²). Take a = c² and b = d² and write the above binomial in the factored form (a + b)(a - b).

= (c² + d²)(c² - d²)

Since (c² - d²) is a difference of two squares, it can be factored as (c + d)(c - d).

= (c² + d²)(c + d)(c - d)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.