FACTORS AND GREATEST COMMON FACTORS WORKSHEET

Problem 1 : 

Write the prime factorization of 60 using factor tree and ladder diagram.

Problem 2 : 

Write the prime factorization of 60 using ladder diagram.

Problem 3 : 

Find the GCF of 24 and 60 using the list of factors. 

Problem 4 : 

Find the GCF of 18 and 27 using prime factorization. 

Problem 5 : 

3x³ and 6x²

Problem 6 : 

4x² and 5y³

Problem 7 : 

Joseph is creating a Web page that offers electronic greeting cards. He has 24 special occasion designs and 42 birthday designs. The cards will be displayed with the same number of designs in each row. Special occasion and birthday designs will not appear in the same row. How many rows will there be if Joseph puts the greatest possible number of designs in each row?

Problem 8 :

Two numbers are 63 and 77, their greatest common factor is 7, then their least common multiple is ?

a)  668     b)  693     c)  674      d)  680

Problem 9 :

Find the HCF of 2/3, 1/2, 3/5

a)  6     b)  1/30     c)  1/15      d)  1/10

Problem 10 :

The LCM of two numbers is 4 times their HCF . The sum of LCM and HCF is 100, then the other number is 

a)  5     b)   25      c)  100   d) 125

Problem 11 :

Find the HCF of 0.8, 0.125, 0.625 and 0.5.

a)  0.1      b)  1/40    c)  1/20    d)  1/80

Detailed Answer Key

1. Answer : 

Choose any two factors of 60 to begin. Keep finding factors until each branch ends in a prime factor. 

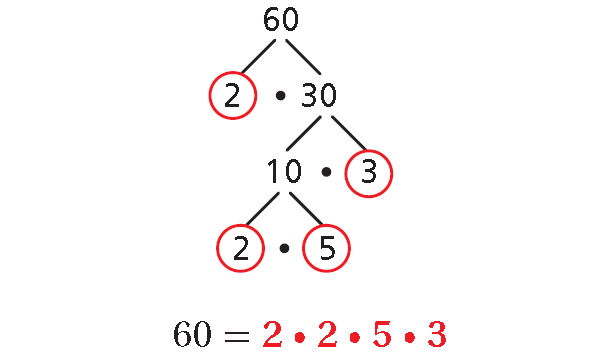
2. Answer :

Choose a prime factor of 60 to begin. Keep dividing by prime factors until the quotient is 1.

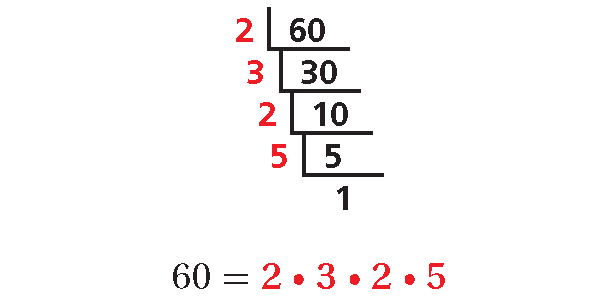
3. Answer : 

Factors of 24 : 1, 2, 3, 4, 6, 8, 12, 24 

Factors of 60 : 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

The GCF of 24 and 60 is 12. 

4. Answer :

18 : 2 ⋅ 3 ⋅ 3

27 : 3 ⋅ 3 ⋅ 3

3 ⋅ 3  =  9

The GCF of 18 and 27 is 9. 

5. Answer : 

Write the prime factorization of each coefficient and write powers as products.

3x³  =  2 ⋅ 3 ⋅ x ⋅ x ⋅ x

3x²  =  2 ⋅ 3 ⋅ x ⋅ x

Find the product of the common factors.

3 ⋅ x ⋅ x  =  3x²

The GCF of 3x³ and 6x² is 3x².

6. Answer : 

Write the prime factorization of each coefficient and write powers as products.

4x²  =  2 ⋅ 2 ⋅ x ⋅ x

5y³  =  5 ⋅ y ⋅ y ⋅ y

There are no common factors other than 1.

The GCF of 4x² and 5y³ is 1. 

7. Answer :

The 24 special occasion designs and 42 birthday designs must be divided into groups of equal size. The number of designs in each row must be a common factor of 24 and 42.

Factors of 24 : 1, 2, 3, 4, 6, 8, 12, 24 

Factors of 42 : 1, 2, 3, 6, 7, 14, 21, 42

The GCF of 24 and 42 is 6.

The greatest possible number of designs in each row is 6. Find the number of rows of each group of designs when there are 6 designs in each row.

24 special occasion designs / 6 designs per row  =  4 rows

42 birthday designs / 6 designs per row  =  7 rows

When the greatest possible number of designs is in each row, there are 11 rows in total.

8. Answer :

When p and q are given numbers, there is some relationship exists between their least common multiple and highest common factors.

p x q = lcm x gcf

Here p = 63 and q = 77, gcf = 7

lcm = (p x q)/gcf

= (63 x 77) / 7

= 63 x 11

= 693

So, their least common multiple is 693. Option b is correct.

9. Answer :

2/3, 1/2, 3/5

HCF of fractions = HCF of numerators / LCM of denominators ---(1)

Numerators are 2, 1 and 3

HCF of numerators = 1

Denominators are 3, 2 and 5

LCM of denominators = 30

Applying these values in (1), we get

= 1/30

10. Answer :

The LCM of two numbers is 4 times their HCF . The sum of LCM and HCF is 100, then the other number is 

LCM = 4(HCF)

LCM + HCF = 100

Applying the value of LCM, we get

4(HCF) + HCF = 100

5 (HCF) = 100

HCF = 100/5

HCF = 25

So, the HCF of these two numbers should be 25, which is option b.

11. Answer :

Given numbers are 0.8, 0.125, 0.625 and 0.5.

By converting each decimal as fractions,

0.8 = 8/10 ==> 4/5

0.125 = 125/1000 ==> 1/8

0.625 = 625/1000 ==> 5/8

0.5 = 5/10 ==> 1/2

HCF of fractions = HCF of numerators / LCM of denominators ---(1)

Numerators are 4, 1 and 5

HCF of numerators = 1

Denominators are 2, 5 and 8

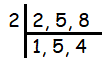
LCM of denominators = 2 x 5 x 4

= 40

Applying these values in (1), we get

= 1/40

So, option b is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.