TWO CIRCLES ARE TOUCHING EACH OTHER

Concentric Circles :

Two or more circles having same center is called the concentric circles. 

Circles touching each other:

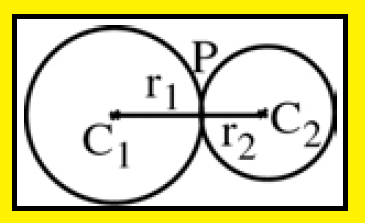
Two circles may touch each other either internally or externally. Let C₁, C₂ be the centers of the circle and r₁, r₂ be their radii and P the point of contact.

Case (1) :

The two circles touch externally :

The distance between their centers is equal to the sum of their radii.

C₁C₂  =  r₁ + r₂

Case (2) :

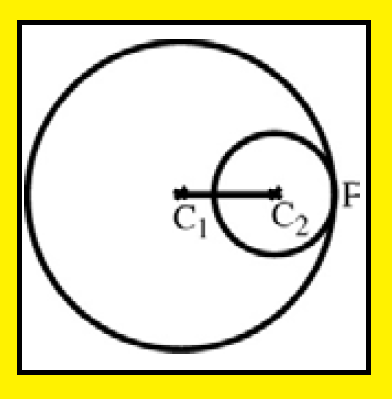
The two circles touch internally :

The distance between their centers is equal to the difference of their radii.

C₁ C₂  =  C₁P − C₂P  =  r₁ − r₂

Orthogonal circles :

Two circles are said to be orthogonal if the tangent at their point of intersection are at right angles.

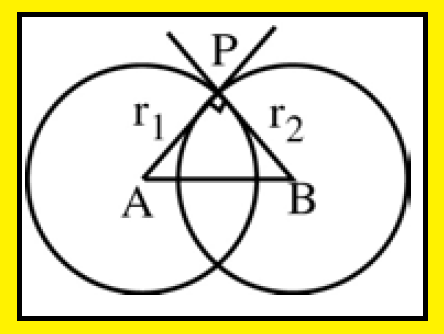
2g₁ g₂ + 2f₁ f₂ = c₁ + c₂

Example 1 :

Find the equation of the circle, which is concentric with the circle 

x² + y² − 4x − 6y − 9 = 0

and passing through the point (−4, −5).

Solution :

Since the given circle and the required circle are concentric, they will have same center.

x² + y² − 4x − 6y − 9 = 0 comparing the equation of general form

x²+y²+2gx+2fy+c  =  0

we get,

2g  =  -4, g  =  -2

2f  =  -6, f  =  -3

Center of given and required circles is (2, 3).

The required circle is passing through the point (-4, -5).

Distance between center and any point on the circle  =  radius

=  √(x₂-x₁)² + (y₂-y₁)²

=  √(2+4)² + (3+5)²

=  √(6²+8²)

=  √100

r  =  10

Required equation of circle :

(x-h⁾²+(y-k)²  =  r²

(x-2⁾²+(y-3)²  =  10²

By expanding we get,

x²+y²-2x-6y+4+9-100  =  0

x²+y²-2x-6y-87  =  0

Example 2 :

Show that the circles 

x²+y²−2x+6y+6  =  0

and

x²+y²−5x+6y+15  =  0

touch each other.

Solution :

By comparing the 1^st equation with general form of the circle, we get

2g₁  =  -2 ==> g₁  =  -1

2f₁  =  6 ==> f₁  =  3 and c₁  =  6

Center of the first circle (1, -3).

Radius  =  √g²+f²-c

r₁  =  √1+9-6

r₁  =  2

By comparing the 2^nd equation with general form of the circle, we get

2g₂  =  -5 ==> g₂  =  -5/2

2f₂  =  6 ==> f₂  =  3 and c₂  =  15

Center of the first circle (5/2, -3).

Radius  =  √g²+f²-c

r₂  =  √(25/4)+9-15

r₂  =  √(25/4)-6

r₂  =  1/2

r1 - r2  =  2 - 1/2

r1 - r2  =  3/2-------(1)

Distance between centers :

C₁(1, -3) and C₂(5/2, -3).

C₁C₂  =  √(x₂-x₁)² + (y₂-y₁)²

C₁C₂  =  √(1-(5/2))² + (-3+3)²

C₁C₂  =  √(-3/2)²

C₁C₂  =  3/2 ------(2)

Since the above circles satisfies the condition 

C₁C₂  =  r₁−r₂

the above circles are intersecting each other internally.

Example 3 :

Show that the circle

x²+y²−8x − 6y + 21  =  0

is orthogonal to the circle

 x²+y²−2y−15   =   0

Solution :

From 1^st equation,

x²+y²−8x − 6y + 21  =  0

2g₁  =  -8 ==> g₁  =  -4

2f₁  =  -6 ==> f₁  =  -3

c₁  =  21

From 2^nd equation,

 x²+y²−2y−15   =   0

2g₂  =  0

2f₂  =  -2 ==> f₂  =  -1

c₂  =  -15

If two circles are intersecting orthogonally, then

2g₁ g₂ + 2f₁ f₂ = c₁ + c₂

2(-4)(0) + 2(-3) (-1) = 21-15

6  =  6

Example 4 :

Circle P has center (-4, -1) and radius 2 units, circle Q has equation x² + y² - 2x + 6y + 1 = 0. Show that the circles P and Q do not touch.

Solution :

Calculating radius of circle Q :

x² + y² - 2x + 6y + 1 = 0

2g = -2, g = -1

2f = 6, f = 3

Center (-g, -f) ==> (1, -3)

c = 1

radius = √g² + f² - c

= √(-1)² + 3² - 1

= √(1 + 9 - 1)

r = 3

Radius of circle P :

radius = 2

Distance between two centers :

ch

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.