FIND A COTERMINAL ANGLE BETWEEN 0° AND 360°

Example 1 :

For each given angle, find a coterminal angle with measure of θ such that 0° ≤ θ < 360°.

(i) 395°  (ii) 525°  (iii) 1150°  (iv) -270°  (v) -450°

Solution :

(i) 395° 

Write 395° in terms of 360°.

395°  =  360° + 35°

So, the coterminal angle of 395° is 35^◦

(ii) 525°

Write 525° in terms of 360°.

525°  =  360° + 165° 

So, the coterminal angle of 525° is 165°.

(iii) 1150°

Write 1150° in terms of 360°.

1150°  =  3(360°) + 70° 

So, the coterminal angle of 1150° is 70°.

(iv) -270°

Write -270° in terms of 360°.

-270°  =  -360° + 90°

So, the coterminal angle of 270° is 90°.

(v) -450°

Write -450° in terms of 360°.

-450°  =  -360° - 90° 

So, the coterminal angle of 450° is -90°. 

How to determine the quadrant of an angle?

Positive Angle Quadrant :

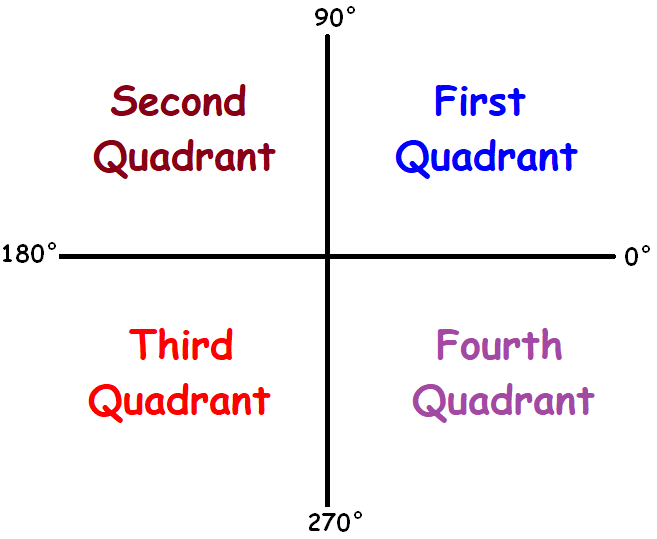
Angle lies between 0° and 90° -----> 1^st quadrant

Angle lies between 90° and 180° -----> 2^nd quadrant

Angle lies between 180° and 270° -----> 3^rd quadrant

Angle lies between 270° and 360° -----> 2^th quadrant

Negative Angle Quadrant :

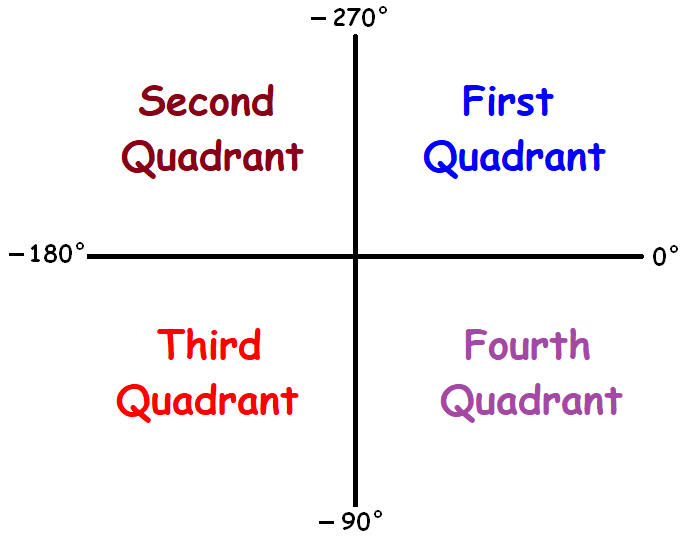
Angle lies between 0° and -90° -----> 4^th quadrant

Angle lies between -90° and -180° -----> 3^rd quadrant

Angle lies between -180° and -270° -----> 2^nd quadrant

Angle lies between -270° and -360° -----> 1^st quadrant

Example 2 :

Identify the quadrant in which an angle of each given measure lies

(i) 25° (ii) 825° (iii) −55°

Solution :

(i) 25° 

25° lies between 0° and 90°.

So, 25° lies in the first quadrant.

(ii) 825°

If the given angle measures more than 360°, then we have to divide the given angle by 360 and find the quadrant for the remaining angle.

When 825° is divided by 360°, the remainder is 105°. 

105° lies between 90° and 180°. 

So, 105° lies in the second quadrant. 

(i) -55° 

-55° lies between -90° and 0°.

So, -55° lies in the fourth quadrant.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.