FIND ANGLES OF ISOSCELES TRIANGLE

An isosceles triangle is a triangle in which two sides are equal in length.

The two sides which are having equal measures will have equal angles.

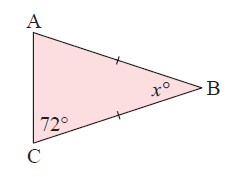
Example 1 :

Solution :

Since AB  =  BC, <C  =  <A

The Sum of interior angles of a triangle is 180˚

So, <A + <B + <C  =  180˚

72˚+x˚+72˚  =  180˚

144˚+x˚  =  180˚

x  =  36˚

<B  =  36˚

So, the missing angle x is 36˚.

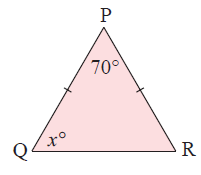
Example 2 :

Solution :

Since PQ  =  PR, <PQR  =  <PRQ  =  x

So, <P + <Q + <R  =  180˚

70˚ + x˚ + x˚   =  180˚

70˚ + 2x˚  =  180˚

2x˚  =  180˚ - 70˚

x  =  110/2

x  =  55˚

<Q  =  <R  =  55˚

<Q  =  55˚ and <R  =  55˚

So, the missing angle x is 55˚

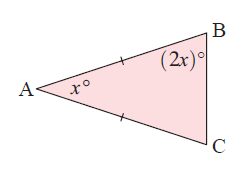
Example 3 :

Solution :

Since AB  =  AC, <B  =  <C

<B  =  <C  =  (2x)˚

The Sum of interior angles of a triangle is 180˚

So, <A + <B + <C  =  180˚

x˚ + 2x˚ + 2x˚  =  180˚

x˚ + 4x˚  =  180˚

5x˚  =  180˚

x˚  =  180/5

x  =  36˚

So, the missing angle x is 36˚

Example 4 :

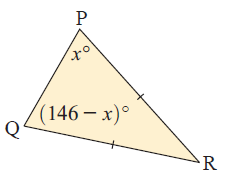
Since RQ  =  RP

<P  =  <Q

x˚  =  (146 – x)˚

x  =  146 – x

x + x  =  146

2x  =  146

x  =  146/2

x  =  73˚

So, the missing angle x is 73˚.

Example 5 :

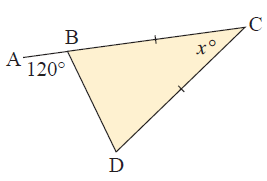
Solution :

<B  =  <D

<DBC + <DBA  =  180˚ (linear pair of angles)

<DBC + 120˚  =  180˚

<DBC  =  180˚-120˚

<DBC  =  60˚

<B  =  60˚

<B  =  <D  =  60˚

The Sum of interior angles of a triangle is 180˚

<C + <B + <D  =  180˚

x˚ + 60˚ + 60˚  =  180˚

x˚ + 120˚  =  180˚

x  =  180˚ - 120˚

x  =  60˚

So, the missing angle x is 60˚.

Example 6 :

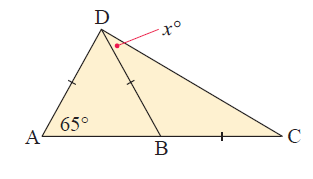
Solution :

Since AD  =  DB, ∆ABC is an isosceles triangle.

DB  =  BC, ∆DBC is an isosceles triangle.

<DAB  =  <DBA  =  65

<DBA + <DBC  =  180

65 + <DBC  =  180

<DBC  =  115

In triangle DBC.

Let x be <BCD and <CDB

<DBC + <BCD + <CDB  =  180

115 + x + x  =  180

2x  =  180-115

2x  =  65

x  =  32.5

Example 7 :

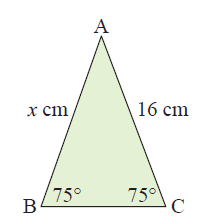
Solution :

Since <B  =  <C  =  75˚

AB  =  x cm, AC  =  16 cm

AB  =  AC

x  =  16 cm

Example 8 :

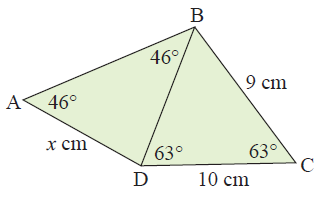
Solution :

DA  =  DB

BD  =  9 cm

So,

x  =  BD

x  =  9 cm and DA  =  9 cm

Example 9 :

Solution :

∆ABC is an isosceles triangle (AB  =  AC).

 base <B  =  <C are equal.

M is the midpoint of the angle bisects the base at right angles.

<AMC  =  <AMB  =  90˚

x  =  90˚

Example 10 :

The figure alongside has not been drawn accurately:

a) Find x.

b) What can be deduced about the triangle?

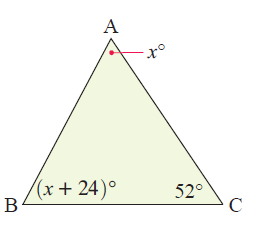
Solution :

(a)  <A + <B + <C  =  180

x + x + 24 + 52  =  180

2x + 76  =  180

2x  =  104

x  =  52

(b)  In the above triangle, two angles are equal. So it is isosceles triangle.

Example 11 :

The degree measure of the vertex angle is (7x - 27).  The degree measure for each base is (9x - 34) . What is the value of one base angle?

Solution :

Vertex angle = 7x - 27

One base angle = 9x - 34

Other base angle will also be the same.

7x - 27 + 2(9x - 34) = 180

7x - 27 + 18x - 68 = 180

25x - 95 = 180

25x = 180 + 95

25x = 275

x = 275/25

x = 11

Applying this value in 9x - 34 

= 9(11) - 34

= 99 - 34

= 65 degree

Example 12 :

The ratio of the measure of a base angle in an isosceles triangle to the measure of the vertex angle is 2:16. Find the measure of each angle.

Solution :

Let base angles be 2x and vertex angle be 16x

2x + 2x + 16x = 180

4x + 16x = 180

20x = 180

x = 180/20

x = 9

2x = 2(9) ==> 18

16x = 16(9) = 144

So, the required angles are 18, 18 and 144.

Example 13 :

The degree measure of the vertex angle is (x + 21). The degree measure for each base is (2x + 17) . What is the value of x?

Solution :

Vertex angle = x + 21

Base angle = 2x + 17

x + 21 + 2(2x + 17) = 180

x + 21 + 4x + 34 = 180

5x + 55 = 180

5x = 180 - 55

5x = 125

x = 125/5

x = 25

So, the value of x is 25.

Example 14 :

The vertex angle of an isosceles triangle is 76 . The degree measure for each base . What is the measure of one base angle?

Solution :

The vertex angle = 76

Measure of each base = x

x + x + 76 = 180

2x = 180 - 76

2x = 104

x = 104/2

x = 52

Example 15 :

The ratio of the measure of a base angle in an isosceles triangle to the measure of the vertex angle is 1:7. Find the measure of each angle.

Solution :

The ratio between base angle and vertex angle is 1 : 7, then the angles are x  and 7x

x + x + 7x = 180

9x = 180

x = 180/9

x = 20

Each angles are 20, 20 and 140.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.