FIND AREA BETWEEN TWO CURVES EXAMPLES

Consider the region S that lies between two curves y  =  f(x) and y  =  g(x) and between the vertical lines x = a and x = b, where f and g are continuous functions and f(x)  ≥ g(x) for all in x [a, b].

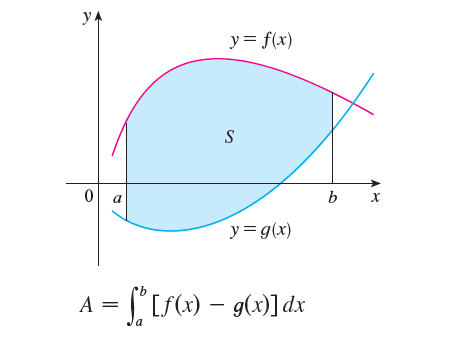
Example 1 :

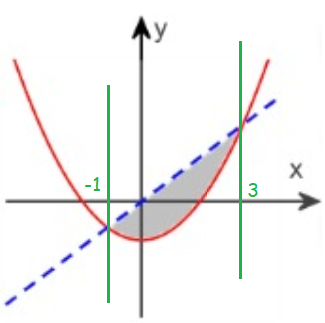
In the figure given below, the equation of the solid parabola is y  =  x² - 3 and the equation of the dashed line is y  =  2x. Determine the area of the shaded region.

Solution :

Let us find the point of intersection,

y  =  x² - 3  ----(1)

y  =  2x  ----(2)

(1)  =  (2)

x² - 3  =  2x

x² - 2x - 3  =  0

(x - 3) (x + 1)  =  0

x  =  3 and x  =  -1

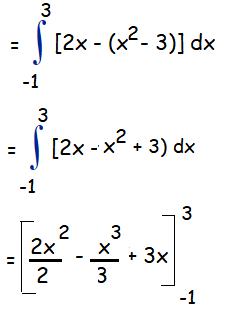
  =  [9 - (27/3) + 9] - [1 + (1/3) - 3]

  =  9 - (3 + 1 - 9)/3

  =  9 + (5/3)

  =  (27 + 5)/3

  =  32/3

So, the required area is 32/3.

Example 2 :

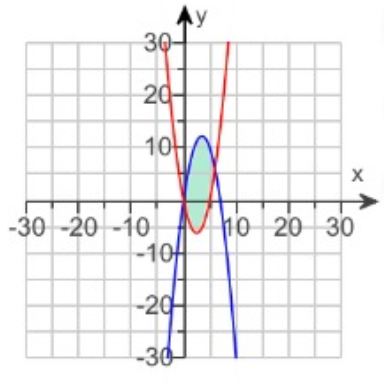
Determine the area of the shaded region bounded by

y  =  -x² + 7x and y  =  x² - 5x

Solution :

y  =  -x² + 7x -----(1)

y  =  x² - 5x -----(2)

(1)  =  (2)

 -x² + 7x  =  x² - 5x 

-2x²  =  -5x - 7x

-2x²  =  -12x

x² - 6x  =  0

x(x - 6)  =  0

x  =  0 and x  =  6

The x-coordinates of point of intersection of the above curves are 0 and 6..

To find the required area, we should subtract the area below the parabola which is open upward from the area of the below the parabola which is open downward.

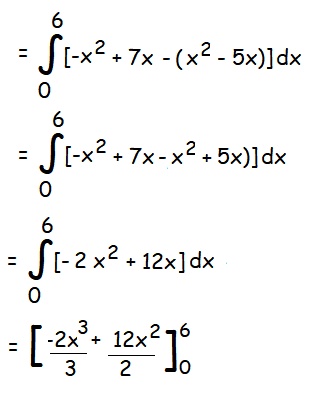
  =  -2(216)/3 + 6(36) - 0

  =  (-512/3) + 216

  =  (-512 + 648)/3

  =  136/3

Example 3 :

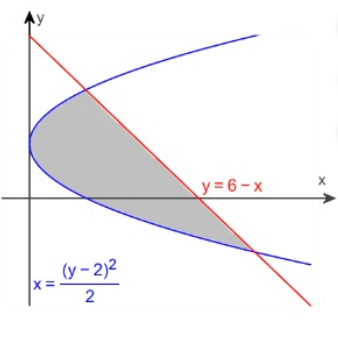
In the graph given below, the equation of the parabola is

x  =  (y-2)²/2

and the equation of the line

y  =  6-x.

Determine the area of the shaded region.

x  =  (y - 2)²/2  ----(1)

x  =  6 - y ----(2)

(1)  =  (2)

(y - 2)²/2  =  6 - y

(y - 2)²  =  2(6 - y)

y² - 4y + 4  =  12 - 2y

y² - 2y - 8  =  0

(y - 4) (y + 2)  =  0

y  =  4 and y  =  -2

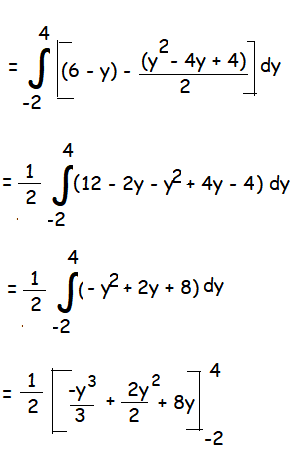
  =  (1/2) [(-64/3 + 16 + 32) - (8 + 4 - 16)]

  =  (1/2) [(-64/3 + 48) - (-4)]

  =  (1/2) (-64/3 + 52)

  =  (1/2)[(-64 + 156)/3]

  =  (1/2)(92/3)

  =  31/3

Example 4 :

Example 4 :

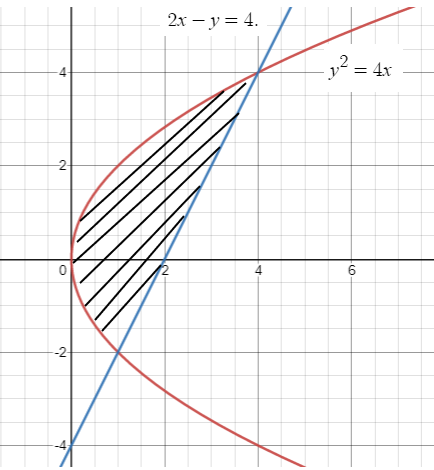
Find the area of the region bounded by the parabola

y²  =  4x

and the line

2x-y = 4

Solution : 

To find the point of intersection, we have to solve the equations.

x  =  y²/4   ------ (1)

x  =  (4+y)/2 ------ (2)

(1)  =  (2)

y²/4  =  (4 + y)/2

2y²  =  4(4 + y)

2 y²  =  16 + 4 y

2y²-4y-16  =  0

now we are going to divide the whole equation by 2,

y²-2y-8  =  0

(y-4) (y+2)  =  0

y-4  =  0          y+2  =  0

y  =  4              y  =  -2

Point of intersection of two curves are (0, 4) (0, -2).

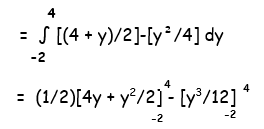
=  [(32+16)/4 - (64/12) ] - [ (-16 + 4)/4 - (-8/12) ]

=  [(48/4) - (16/3)] - [(-12/4) - (-8/12)]

=  [12-(16/3)] - [-3 + (2/3)]

=  [(36-16)/3)] - [(-9+2)/3]

=  [20/3] - [-7/3]

=  (20/3) + (7/3)

=  (20+7)/3

=  27/3

=  9 square units 

Example 5 :

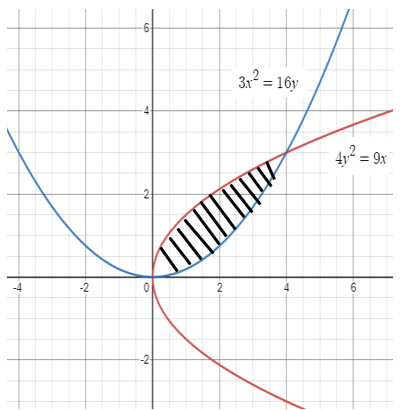
Find the common area enclosed by the parabolas

4y²  =  9x

and

3x²  =  16y

Solution :

4y²  =  9x ---(1)

3x²  =  16y  ---- (2)

y  =  (3 √x)/2

y  =  3x²/16

y  =  y

(3√x)/2  =  3x²/16

48 √x  =  6x²

(48/6)√x  =  x²

8 √x  =  x²

√x  =  x²/8

taking squares on both sides

x  =  x⁴/64

64  =  x⁴/x

 64  =  x³

4³  =  x³

x  =  4

y  =  3 (4)²/16

y  =  3

Point of intersection are (0, 0) and (4, 3).

To find the required area that is shaded portion, we have to subtract the area which is open upward from the area which is open rightward.

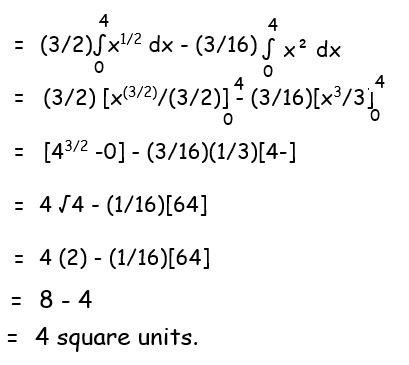
Example 6 :

Find the area of the circle whose radius is a

Solution :

Equation of circle :

x² + y² = a²

y²  =  a²-x²

y  =  √(a²-x²)

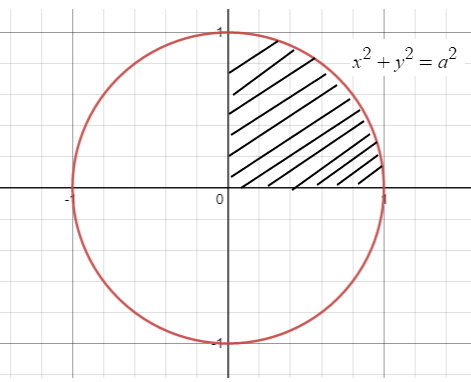
Required area  =  4  integral to 0 to a √(a² - x²) dx

=  4  [(x/2)√(a² - x²) + a²/2 sin⁻¹ (X/a)]       

=  4[(a/2)√(a² - a²) + (a²/2) sin⁻¹ (a/a)] - 0 - 0]

=  4[0 + (a²/2) sin⁻¹ (1)]

=  4[0 + (a²/2) (π/2)]

=  4[(πa²/4)]

=  π a² square units

Therefore the required area of circle is πa² square units.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.