FIND AREA OF QUADRILATERAL WITH VERTICES

Let us consider the quadrilateral ABCD shown below. 

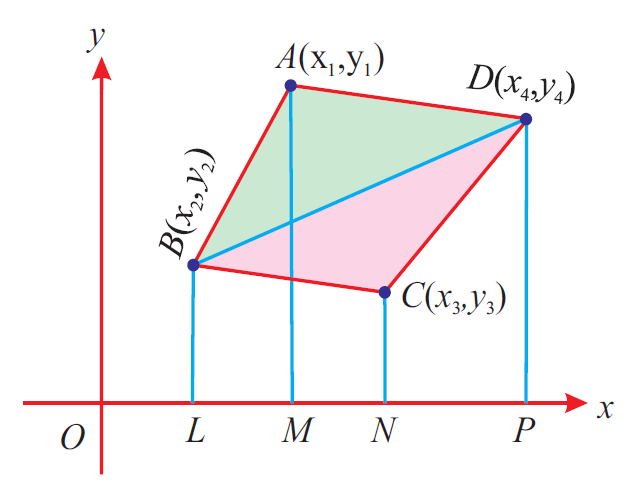
In the above quadrilateral, A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) and D(x₄, y₄) are the vertices.

To find area of the quadrilateral ABCD, now we have take the vertices A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) and D(x₄, y₄) of the quadrilateral ABCD in order (counter clockwise direction) and write them column-wise as shown below. 

Add the diagonal products x₁y₂, x₂y₃, x₃y₄ and x₄y₁ are shown in the dark arrows.

(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁) -----(1)

Add the diagonal products x₂y₁, x₃y₂, x₄y₃ and x₁y₄ are shown in the dotted arrows.

(x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄) -----(2)

Subtract (2) from (1) and multiply the difference by 1/2 to get area of the quadrilateral ABCD.

So, area of the quadrilateral ABCD is

=  (1/2) ⋅ {(x₁y₂ + x₂y₃ + x₃y₄ + x₄y₁)

- (x₂y₁ + x₃y₂ + x₄y₃ + x₁y₄)}

Example 1 :

Find the area of the quadrilateral whose vertices are at

(–9, –2), (–8, –4), (2, 2) and (1, –3)

Solution :

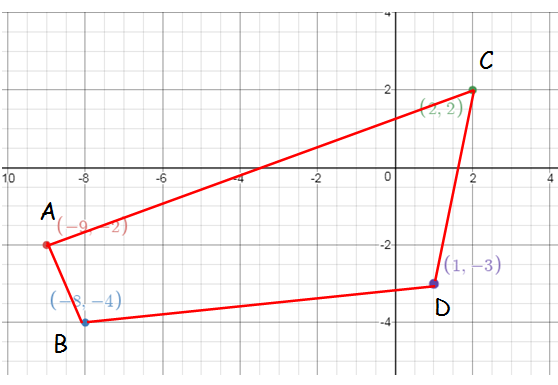
By taking the points in counter clock wise, we have to find the area of CABD.

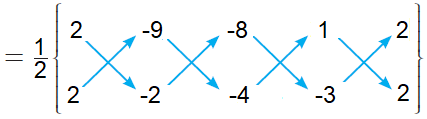
= (1/2)[(-4 + 36 + 24 + 2) - (-18 + 16 - 4 - 6)]

= (1/2)[(62-4) - (-28 + 16)]

= (1/2)[58 - (-12)]

 = (1/2)(58 + 12)

= (1/2)(70)

= 35 square units.

Example 2 :

Find the area of the quadrilateral whose vertices are at

(–9, 0), (–8, 6), (–1, –2) and (–6, –3)

Solution :

By plotting the given points in the graph paper, we get

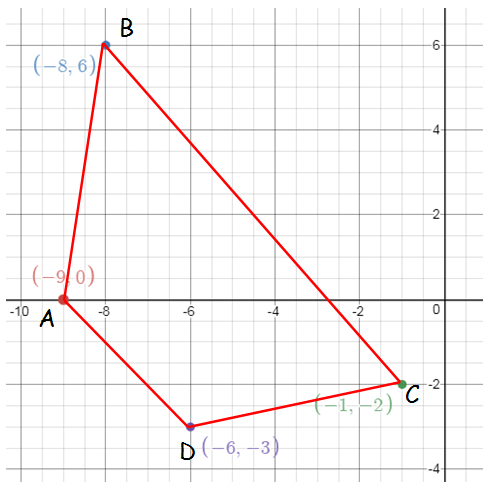
By taking the points in counter clock wise direction, we find the area of BADC.

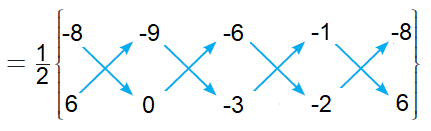
= (1/2)[(0 + 27 + 12 - 6) - (-54 + 0 + 3 + 16)]

= (1/2)[(39 - 6) - (-54 + 19)]

= (1/2)[(33) - (-35)]

= (1/2)(33 + 35)

= (1/2) (68)

  = 34 square units.

Example 3 :

Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (–4, –2), (–3, k), (3, –2) and (2, 3)

Solution :

Area of quadrilateral = 28 square units

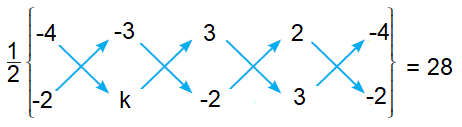
[(-4k  + 6 + 9 - 4) - (6 + 3k - 4 - 12)] = 28(2)

(-4k + 11) - (3k - 10) = 56

-4k + 11 - 3k + 10 = 56

-7k = 56 - 21

-7k = 35

k = 35/(-7)

k = -5

Example 4 :

If the points A(-3, 9), B(a, b) and C(4, -5) are collinear and if a + b = 1, then find a and b.

Solution :

a + b = 1 ----(1)

Because the given points are collinear, 

area of triangle = 0

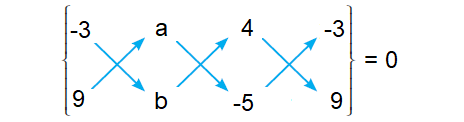
[(-3b - 5a + 36) - (9a + 4b + 15)] = 0

-3b - 5a + 36 - 9a - 4b - 15 = 0

-5a - 9a - 3b - 4b + 21 = 0

-14a - 7b + 21 = 0

2a + b = 3 ----(2)

(2) - (1) : 

2a + b - (a + b) = 3 - 1

2a - a + b - b = 2

a = 2

Substitute a = 2 in (1).

2 + b = 1

b = -1

Example 5 :

If the area of the quadrilateral whose angular points, taken in order, are (1, 2), (–5, 6), (7, –4), (p, –2) be zero, find the value of p.

Solution :

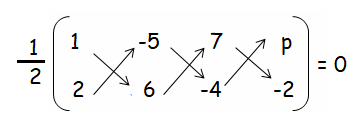
(6 + 20 - 14) - (-10 + 42 - 4p) = 0(2)

(26 - 14) - (32- 4p) = 0

12 - (32 - 4p) = 0

12 - 32 + 4p = 0

-20 + 4p = 0

4p = 20

p = 20/4

p = 5

So, the value of p is 5.

Example 6 :

Find the area of the quadrilateral 𝐴𝐵𝐶𝐷 whose vertices are 𝐴(−3, −1), 𝐵(−2, −4), 𝐶(4, −1) and 𝐷(3, 4).

Solution :

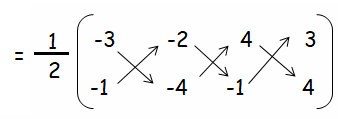
= (1/2) [(12 + 2 + 16) - (2 - 16 - 3)]

= (1/2) [30 - (2 - 19)]

= (1/2) [30 - (-17)]

= (1/2) [30 + 17]

= (1/2) (47)

= 23.5 square units.

Example 7 :

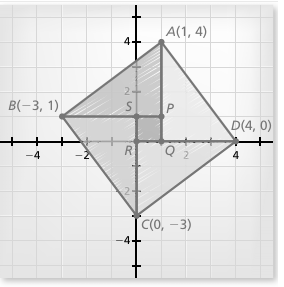
a. Quadrilateral ABCD is partitioned into four right triangles and one square, as shown. Find the coordinates of the vertices for the five smaller polygons.

b. Find the areas of the five smaller polygons. Area of Triangle BPA: Area of Triangle AQD: Area of Triangle DRC: Area of Triangle CSB: Area of Square PQRS:

c. Is the sum of the areas of the five smaller polygons equal to the area of quadrilateral ABCD? Justify your answer.

Solution :

a) P (1, 1), Q (1, 0) R (0, 0) and S(0, 1)

b) Area of triangle AQD :

Base = |4 - 1| ==> 3

Height = |4 - 0| ==> 4

Area of triangle = (1/2) x base x height

= (1/2) x 3 x 4

= 3 x 2

= 6 square units.

Area of triangle APB :

Base = |-3 - 1| ==> |-4| ==> 4

Height = |4 - 1| ==> 3

Area of triangle = (1/2) x 4 x 3

= 2 x 3

= 6 square units

Area of triangle BSC :

Base = |-3 - 0| ==> 3

Height = |-3 - 1| ==> 4

Area of triangle = (1/2) x 4 x 3

= 2 x 3

= 6 square units

Area of square PQRS :

Side length of square = 1 unit

Area of square = 1²

= 1 square units

Area of quadrilateral ABCD :

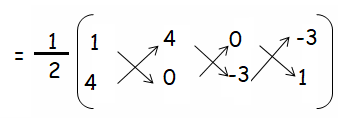
= (1/2)[(1 - 12 + 0) - (16 + 0  + 9)]

= (1/2) [-11 - 25]

= (1/2)(36)

Area of quadrilateral ABCD = 18 square units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.