FIND AREA OF THE SHADED REGION OF A CIRCLE

Example 1 :

The inner part of an athletics track is lawn. Find the area of the lawn.

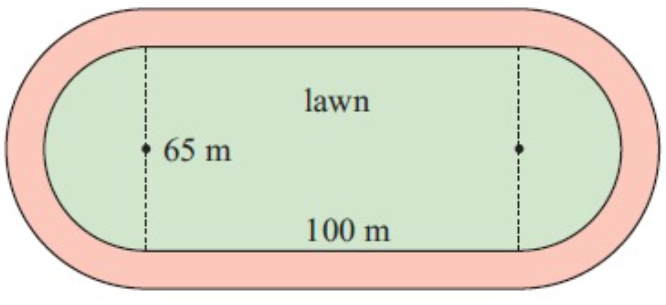
Solution :

Area of lawn

=  Area of rectangle + 2(Area of semicircle)

Length  =  100 m, width  =  65 m

radius  =  65/2  ==>  32.5 m

Area of rectangular lawn  =  Length × width + 2(∏r²/2)

=  (100 × 65) + [22/7 × 32.5 × 32.5]

=  6500 + 3319.64

=  9819.6 m²

Area of shaded region  =  9820 m²

So, area of lawn is 9820 m².

Example 2 :

A door has the dimensions shown.

(a)  How high is the door at its highest point ?

(b)  What is the area of the door in square meters ?

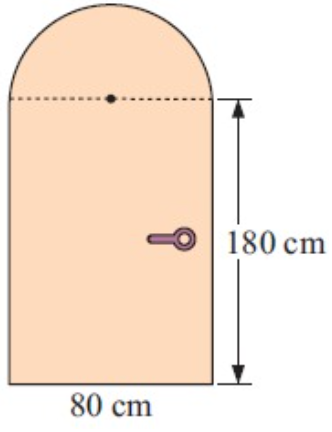
Solution :

(a)  From the picture, the door consist of rectangle and a semicircle.

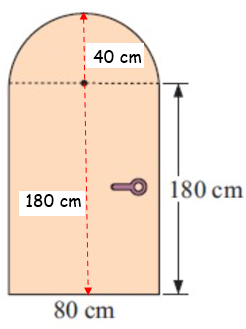
=  (180 + 40) cm

=  220 cm

220 cm high is the door at its highest point.

(b) 

Area of shaded region

=  Area of rectangular door + Area of semicircle

Length  =  180 cm  ==>  1.8 m

Width  =  80 cm  ==>  0.8 m

Diameter (d)  =  80 cm

Radius  =  40 cm  ==>  0.40 m

=  (1.8 × 0.8) + [(22/7 × 0.4 × 0.4)/2]

=  1.44 + 0.2514

=  1.69 m²

So, area of the door is 1.69 m².

Example 3 :

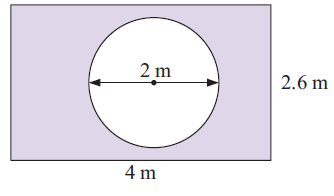
Find the area of the shaded region.

Solution :

Area of shaded region

=  Area of rectangle - Area of circle

Length  =  4 m, Width  =  2.6 m

d  =  2 m and r  =  1 m

Area of shaded region  =  Length × width - ∏r²

=  (4 × 2.6) - (22/7 × 1 × 1)

=  (10.4 – 3.14) m²

Area of shaded region  =  7.26 m²

So, area of the shaded region given above is 7.26 m².

Example 4  :

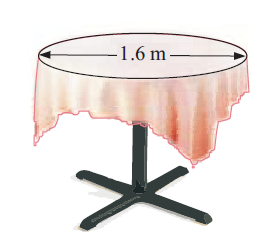
A circular table top has a diameter of 1.6 m. A rectangular tablecloth 2 m by 2 m is placed over the table top. What area of the tablecloth overlaps the table ?

Solution :

Overlapping area

=  Area of rectangular tablecloth - Area of circular table top

Length  =  2 m, width  =  2 m

Diameter d  =  1.6 m and radius  =  0.8 m

Overlapping area  =  Length × width -  ∏r²

=  (2 x 2) - (22/7 × 0.8 × 0.8)

=  (4 - 2.0114) m²

Overlapping area  =  1.98 m²

So, Area of the tablecloth is 1.98 m²

Example 5 :

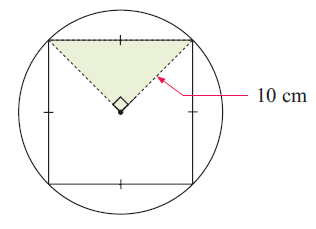
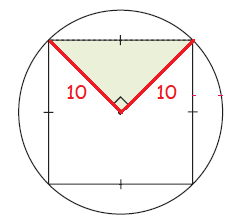
Consider a square within a circle. 

(a)  Find the area of:

i) the circle

ii) the shaded triangle

iii) the square.

(b) What percentage of the circle is occupied by the square ?

Solution :

(i)  From the picture given radius of the circle is 10 cm.

Area of circle  =  ∏r²

=  (22/7 × 100) cm²

Area of circle  =  314 cm²

(ii) the shaded triangle

By drawing a diagonal for he square, it divides the square into two right triangles.

Area of triangle  =  1/2 ⋅ b ⋅ h

=  1/2 ⋅ 10 ⋅ 10

=  50 cm²

(iii) the square

length of diagonal  =  20 cm

Area of square  =  1/2 . d²

=  1/2 × 20 × 20

Area of square =  200 cm²

  =  200 cm²

(b)  Percentage  =  (Area of square/Area of circle) × 100 

=  (200/314) × 100

=  0.6369 × 100

=  63.69%

So, 63.7% of circle is occupied by the square.

Example 6 :

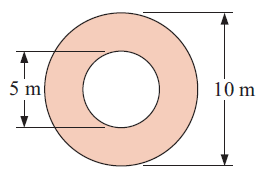
(a)  Find the shaded area.

(b) Find the sum of the perimeters of the two circles.

Solution :

(a)  Area of shaded region

=  Area of large circle – Area of small circle

Let "R" and "r" be the radius of large and small circles.

R  =  10/2  ==>  5 m

r  =  5/2

Area of shaded region  =  Area of large circle - Area of small circle

=  ∏R² - ∏r²

=  ∏(25-(5/2)²)

=  ∏(25-(25/4))

=  (22/7)(75/4)

Area of shaded region  =  58.92 m²

b)  Sum of the perimeters of the two circles

=  Perimeter of large circle + Perimeter of small circle

=   2∏R+ 2∏r

=  2∏(R+r)

=  2(22/7)(5+5/2)

=  (22/7)(15)

=  47.14 m

The sum of perimeter of circles is 47.14 m.

Example 7 :

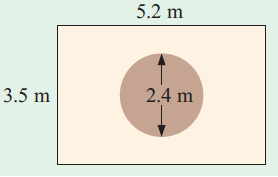
A circular rug is laid on a tiled floor. Find

a) the area of the rug

b) the visible area of the tiled floor.

Solution :

Radius r  =  2.4/2  ==>  1.2 m

Area of rug  =  ∏r²

=  ∏ × 1.2 × 1.2

=  (22/7 × 1.44) m²

=  4.525 m²

Area of rug  =  4.52 m²

b) the visible area of the tiled floor

=  Area of tiled floor – Area of rug

Length  =  5.2 m, Width  =  3.5 m

=  (5.2 × 3.5) - 4.52

=  18.2-4.52

=  13.68 m²

So, the visible area of the tiled floor is 13.68 m²

Example 8 :

A gardener is making a path using 8 cylindrical concrete pavers. Each paver has a radius of 20 cm and is 5 cm thick.

(a)  Find the total area of the tops of the pavers.

(b)  Find the total volume of the pavers

Solution :

Radius of pavers (r)  =  20 cm

r  =  (20/100) m

r  =  0.2 m

Area of top 8 pavers  =  8(∏r²)

=  8(22/7 × 0.2 × 0.2) m²

=  8(0.125) m²

=  1.005 m²

=  1.01 m²

Total area of the tops of the pavers is 1.01 m².

b) r  =  0.2 m

height (h)  =  5 cm  ==>  0.05 m

 Volume of the pavers  =  8(∏r²h)

=  8(22/7 × 0.2 × 0.2 × 0.05)

=  8(0.044/7)

=  8(0.006285) m³

=  0.0503 m³

Volume of the pavers  =  0.0503 m³

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.