FIND COMPOSITION OF TWO FUNCTIONS

Definition : 

Let f : A ----> B and g : B ----> C be two functions. Then the composition of f and g denoted by g o f is defined as the function g o f(x) = g[f(x)] for all x ∈ A.

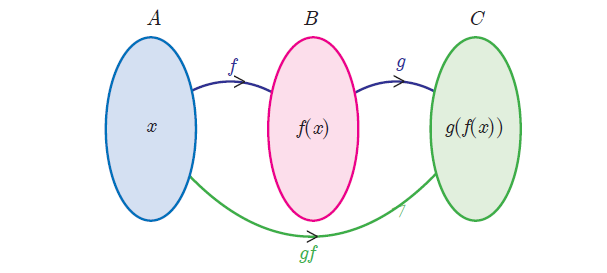
Note : 

Generally, f o g ≠ g o f for any two functions f and g. So, composition of functions is not commutative.

Example 1 :

Find f o g, if f(x) = x and g(x) = 3x².

Solution :

f o g = f[g(x)]

= f[3x²]

= 3x²

Example 2 :

If f(x) = 2x - 5 and g(x) = x + 2 find f o g.

Solution :

f o g = f[g(x)]

= f[x + 2]

= 2(x + 2) - 5

= 2x + 4 - 5

= 2x - 1

Example 3 :

If f(x) = -3x + 4 and g(x) = x² find g o f. 

Solution :

g o f = g[f(x)]

= g[-3x + 4]

= (-3x + 4)²

= (-3x)² + 2(-3x)(4) + 4²

= 9x² - 24x + 16

Example 4 :

If f(x) = 4x² + 2 and g(x) = √(x- 8) find f o g.

Solution :

f o g = f[g(x)]

= f[√(x- 8)]

= 4[√(x- 8)]² + 2

= 4(x- 8) + 2

= 4x - 32 + 2

= 4x - 30

Example 5 :

If f(x) = -9x + 4 and g(x) = x⁴, find g o f.

Solution :

g o f = g[f(x)]

= g[-9x + 4]

= (-9x + 4)⁴

Example 6 :

If f(x) = 2x + 1 and g(x) = x² - 2, then verify f o g = g o f.

Solution :

f o g :

= f[g(x)]

= f[x² - 2]

= 2(x² - 2) + 1

= 2x² - 4 + 1

= 2x² - 3 ----(1)

g o f :

= g[f(x)]

= g[2x + 1]

= (2x + 1)² - 2

= (2x)² + 2(2x)(1) + 1² - 2

= 4x² 4x + 1 - 2

= 4x² 4x - 1 ----(2)

From (1) and (2), we see that f o g ≠ g o f.

Example 7 :

Let f(x) = 2^x and g(x) = x³ - 4x. Find the following.

a) f(g(2))         b)  (g o f)(-1)     c)  g(f(1))

Solution :

Given that f(x) = 2^x and g(x) = x³ - 4x

a) f(g(2))

g(2) = 2³ - 4(2)

= 8 - 8

g(2) = 0

Applying the value of g(2) in  f(g(2))

f(g(2)) = f(0)

To evaluate f(0), we have to apply x = 0 in the function f(x).

f(0) = 2⁰

= 1

So, the value of f(g(2)) is 1.

b)  (g o f)(-1) = g[f(-1)]

Applying -1 for x in the function f(x), we get

f(-1) = 2^-1

= 1/2

Applying the value of f(-1) in g[f(-1)], we get

= g(1/2)

To evaluate g(1/2) in the function g(x)

g(1/2) = (1/2)³ - 4(1/2)

= 1/8 - 2

= (1 - 16)/8

= -15/8

So, the value of (g o f)(-1) is -15/8.

c)  g(f(1))

f(1) = 2¹

= 2

Applying the value of f(1) in  g(f(1))

= g(2)

To evaluate g(2), we apply x = 2 in the function g(x).

g(x) = 2³ - 4(2)

= 8 - 8

= 0

So, the value of g(f(1)) is 0.

Example 8 :

Let f(x) = 4^x and h(x) = f(g(x)). Fill in the table.

Solution :

When x = 1

h(1) = f(g(1))

From the table, the value of g(1) is -1

h(1) = f(-1)

From f(x) = 4^x, we get f(-1) = 4^-1

= 1/4

h(1) = 1/4

When x = 2

h(2) = f(g(2))

From the table, the value of g(2) is 0

h(2) = f(0)

From f(x) = 4^x, we get f(0) = 4⁰

= 1

h(2) = 1

When x = 3

h(3) = f(g(3))

From the table, the value of g(3) is 2

h(3) = f(2)

From f(x) = 4^x, we get f(2) = 4^-2

= 1/4²

= 1/16

h(3) = 1/16

Example 9 :

Let g(x) = √(2x - 1) and h(x) = g(f(x)). Fill in the table.

Solution :

g(x) = √(2x - 1) and h(x) = g(f(x))

When x = 3

h(3) = g(f(3))

From the table, the value of f(3) is 13

= g(13)

Evaluating the value of g(13) :

g(13) =  √(2(13) - 1)

=  √(26 - 1)

=  √25

= 5

When x = 4

h(4) = g(f(4))

From the table, the value of f(4) is 1

= g(1)

Evaluating the value of g(1) :

g(1) =  √(2(1) - 1)

=  √(2 - 1)

=  √1

= 1

When x = 5

h(5) = g(f(5))

From the table, the value of f(5) is 6

= g(6)

Evaluating the value of g(6) :

g(6) =  √(2(6) - 1)

=  √(12 - 1)

=  √11

Example 10 :

a) Find f(g(2))

b)  Find (g o f) (-2)

c)  Find g(f(-4))

Solution :

a) f(g(2))

From the graph, the value of g(2). We get the point (2, -2).

f(g(2)) = f(-2)

From the graph f(x), the point is (-2, 2).

f(g(2)) = 2

b) (g o f) (-2) = g(f(-2))

From the graph f(x), we get the point (-2, 2).

= g(2)

From the graph of g(x), we get the point (2, -2).

g(2) = -2

So, the value of (g o f) (-2) is -2.

c)  g(f(-4)) 

From the graph of f(x), we get the point (-4, 2).

f(-4) = 2

g(f(-4)) = g(2) 

From the graph of g(x), we get the point (2, -2).

So, the value of g(f(-4)) is -2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.