FIND EQUATION OF THE LINE FROM THE GRAPH

Find equation of the line from the following graph given :

Example 1  :

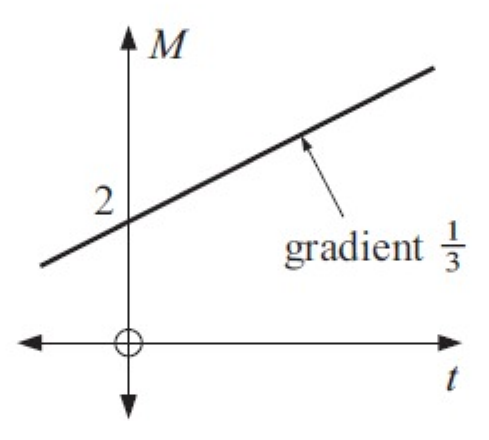
Solution :

Slope of a line  =  1/3

y – intercept(b)  =  2

Equation of a straight line y  =  mx + b

y  =  1/3x + 2

3y  =  x + 6

x – 3y + 6  =  0

So, the required equation is x – 3y + 6  =  0.

Example 2 :

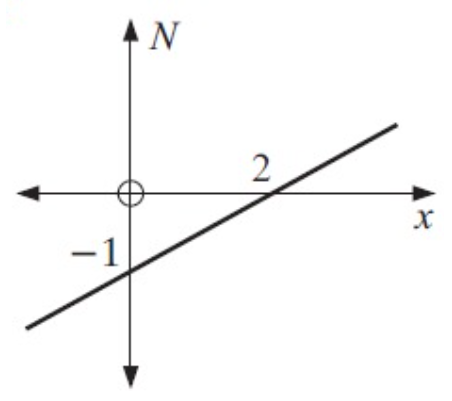
Solution :

x – intercept form a  =  2

N – intercept form b  =  -1

Slope = Rise / run

= 1/2

The point lies on the line is (2, 0)

y = mx + b

N = (1/2)x + (-1)

N = x/2 - 1

Converting into standard form, 

2N = x - 2

x - 2N - 2 = 0

Example 3 :

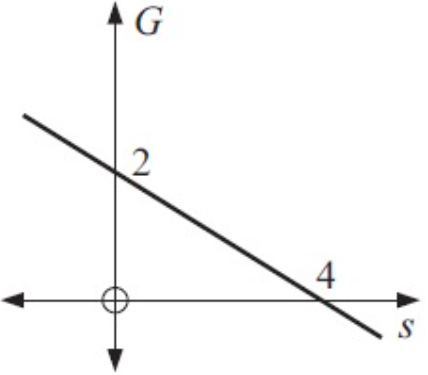
Solution  :

s – intercept form a  =  4

G – intercept form b  =  2

Slope = Rise / run

= -2/4

= -1/2

The point lies on the line is (4, 0)

y = mx + b

G = (-1/2)S + (-1)

G = (-S/2) - 1

2G = -S - 2

S + 2G + 2 = 0

Example 4 :

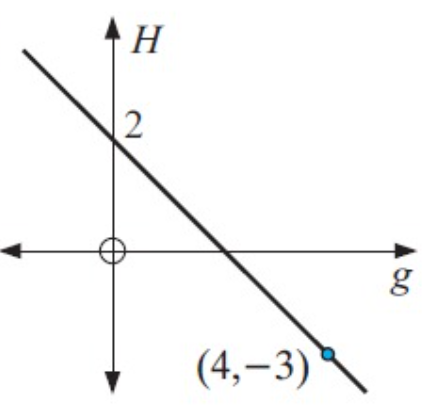
Solution :

From the figure given above, y-intercept is 2. One of the points on the line (4, -3)

y = mx + b

H = mG + b  -----(1)

b = 2 and (x, y) ==> (G, H) is at (4, -3).

-3 = m(4) + 2

-3 = 4m + 2

-3 - 2 = 4m

4m = -5

m = -5/4

By applying the slope and y-intercept, we get

H = (-5/4)G + 2

H = (-5G + 8)/4

4H = -5G + 8

5G + 4H - 8 = 0

Example 5 :

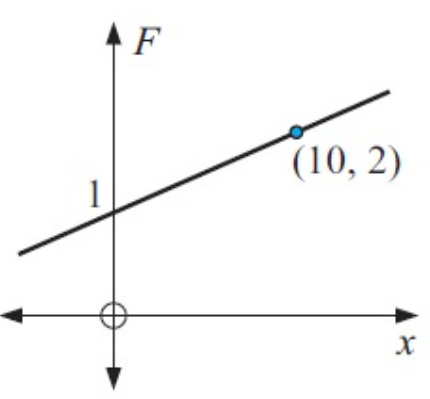
Solution :

From the y-intercept, move right 10 units and move up 1 unit.

Rise = 1 and run = 10

Slope (m) = rise / run

m = 1/10

y = mx + b

F = mx + b

Here y-intercept is 1

F = (1/10) x + 1

F = x/10 + 1

F = (x + 10)/10

10F = x + 10

x + 10F + 10 = 0

Example 6 :

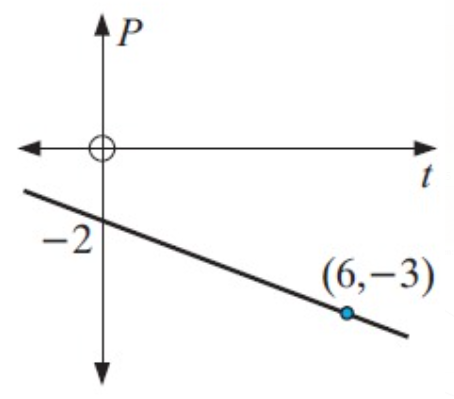
Solution :

By observing the figure, it is shown the y-intercept and points are given. Using these details using the formula

y = mx + b ----(1)

we find the equation.

Here x and y are 6 and -3 respectively, and b = -2

-3 = m(6) + (-2)

-3 + 2 = 6m

-1 = 6m

m = -1/6

Then the slope of the line shown in the graph is -1/6

Applying the slope and y-intercept in (1). we get

y = (-1/6)x + (-2)

Converting into standard form, we get

y = (-x/6) - 2

6y = -x - 12

x + 6y + 12 = 0

Example 7 :

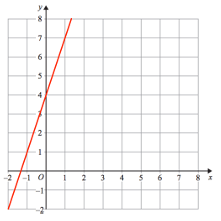
Solution :

By observing the line, we know that y-intercept is at y = 4. The value of b is 4.

From y-intercept,

Rise = 3 and run = 1

Slope (m) = rise / run

m = 3/1 ==> 3

By choosing one of the points on the line, we get (1, 7)

y - y₁ = m(x - x₁)

y - 7 = 3(x - 1)

y - 7 = 3x - 3

3x - y - 3 + 7 = 0

3x - y + 4 = 0

Example 8 :

The graph shows two perpendicular lines A and B.

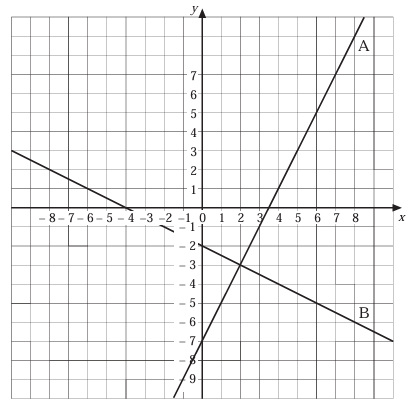
a)  Calculate the gradient of A and write down its equation

b)  Calculate the gradient of B and write down its equation.

c) Describe the gradients of the lines are related.

Solution :

Gradient of line A :

Tracing two points of line A, (4, 1) and (6, 5)

m = (y₂ - y₁) / (x₂ - x₁)

= (5 - 1) / (6 - 4)

= 4/2

= 2

Gradient of line B :

Tracing two points of line A (2, -3) and (6, -5)

m = (y₂ - y₁) / (x₂ - x₁)

= (-5 + 3) / (6 - 2)

= -2/4

= -1/2

Equation of line A :

y - y₁ = m(x - x₁)

Here slope m = 2 and a point is (4, 1)

y - 1 = 2(x - 4)

y = 2x - 4 + 1

y = 2x - 3

Equation of line B :

y - y₁ = m(x - x₁)

Here slope m = -1/2 and a point is (2, -3)

y + 3 = (-1/2)(x - 2)

y + 3 = -x/2 + 1

y = -x/2 + 1 - 3

y = (-x/2) - 2

y = (-x - 4)/2

2y = -x - 4

x + 2y + 4 = 0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.