FIND HORIZONTAL AND VERTICAL ASYMPTOTES
Vertical Asymptote :
The vertical line x = a is called a vertical asymptote of the graph of y = f(x) if
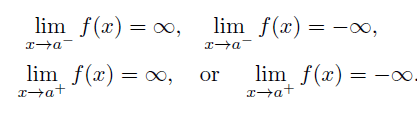
How to find vertical asymptote?
The graph of y = f(x) will have vertical asymptotes at those values of x for which the denominator is equal to zero.
Horizontal Asymptote :
The horizontal line y = b is called a horizontal asymptote of the graph of y = f(x) if either The graph of y = f(x) will have at most one horizontal asymptote. It is found according to the following:
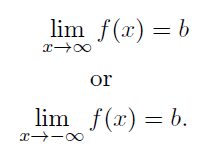
How to find vertical and horizontal asymptotes of rational function?
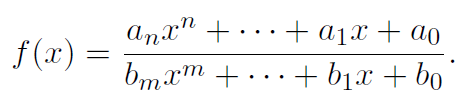
1) If
degree of numerator > degree of denominator
then the graph of y = f(x) will have no horizontal asymptote.
2) If
degree of numerator = degree of denominator
then the graph of y = f(x) will have a horizontal asymptote at y = an/bm.
3) If
degree of numerator < degree of denominator
then the graph of y = f(x) will have a horizontal asymptote at y = 0 (i.e., the x-axis).
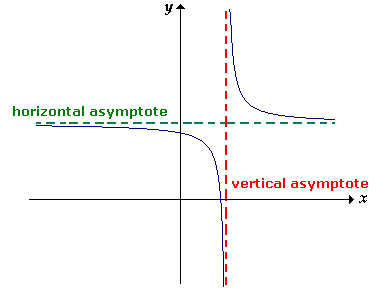
- A graph can have an infinite number of vertical asymptotes, but it can only have at most two horizontal asymptotes.
- Horizontal asymptotes describe the left and right-hand behavior of the graph.
- A graph will (almost) never touch a vertical asymptote; however, a graph may cross a horizontal asymptote.
Find the vertical and horizontal asymptotes of the functions given below.
Example 1 :
f(x) = 4x2/(x2 + 8)
Solution :
Vertical Asymptote :
x2 + 8 = 0
x2 = -8
x = √-8
Since √-8 is not a real number, the graph will have no vertical asymptotes.
Horizontal Asymptote :
The highest exponent of numerator and denominator are equal.
Vertical asymptote y = 4/1.
So, horizontal asymptote is y = 4
Example 2 :
f(x) = (4x+5)/(4x2-9)
Solution :
Vertical Asymptote :
4x2-9 = 0
4x2 = 9
x = √(9/4)
x = ± 3/2
So, vertical asymptotes are x = 3/2 and x = -3/2.
Horizontal Asymptote :
Degree of the denominator > Degree of the numerator
So, the horizontal asymptote is y = 0.
Example 3 :
f(x) = (x3+2x+1)/(x2-x-12)
Solution :
Vertical Asymptote :
x2-x-12 = 0
(x-4)(x+3) = 0
x = 4 and -3
So, vertical asymptotes are x = 4 and x = -3.
Horizontal Asymptote :
Degree of the numerator = 3
Degree of the denominator = 2
Degree of the numerator > Degree of the denominator
It has no horizontal asymptote.
Example 4 :
f(x) = (4x2-3)/(2x2-3x+1)
Solution :
Vertical Asymptote :
2x2-3x+1 = 0
(2x-1)(x-1) = 0
x = 1/2 and 1
So, vertical asymptotes are x = 1/2 and x = 1.
Horizontal Asymptote :
Degree of the numerator = 2
Degree of the denominator = 2
Degree of the numerator = Degree of the denominator
Horizontal asymptote = 4/2 ==> 2
So, the horizontal asymptote is y = 2.
Example 5 :
Find the asymptote of the function
f(x) = ln(2x+3)
Solution :
Vertical Asymptote :
2x+3 = 0
2x = -3
x = -3/2
So, vertical asymptote is x = -3/2.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 144)
Apr 14, 25 07:27 PM
Digital SAT Math Problems and Solutions (Part - 144) -
Quadratic Equation Problems with Solutions (Part - 1)
Apr 14, 25 11:33 AM
Quadratic Equation Problems with Solutions (Part - 1) -
Quadratic Equation Problems with Solutions (Part - 2)
Apr 14, 25 11:22 AM
Quadratic Equation Problems with Solutions (Part - 2)
