FIND INPUT NUMBER FROM THE RULE AND OUTPUT

Given the following output numbers and rules, calculate the corresponding input numbers :

Example 1 :

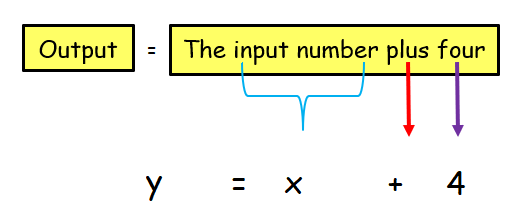
Rule : the input number plus four

Output numbers  {5, 7, 15}

Solution :

Let x and y be the input and output number respectively.

So, the required function is y = x+4

So, input numbers and output numbers are

1 ==> 5, 3 ==> 7, 11 ==> 15

Example 2 :

Double the input number plus two

Output numbers  {2, 4, 10}

Solution :

Let x and y be input and output respectively.

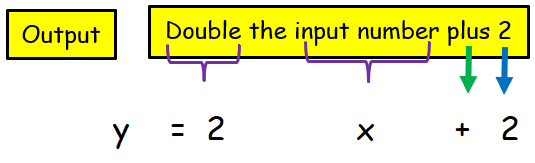
So, the required function is y = 2x+2

So, input numbers and output numbers are

0 ==> 2, 1 ==> 4, 4 ==> 10

Example 3 :

Rule : Five times the input number minus three

Output numbers {7, 12, 17}

Solution :

Let x and y be input and output respectively.

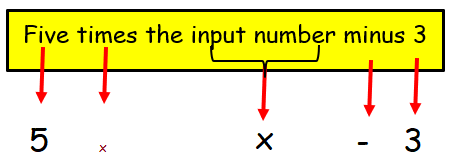
So, the required function is y = 5x-3

So, input numbers and output numbers are

7 ==> 2, 3 ==> 12, 4 ==> 17

Example 4 :

Rule : Add one to the input number then double the result 

Output numbers  {2, 6, 12}

Solution :

Let x and y be input and output respectively.

Add one to the input number  ==>  x+1

double the result ==> 2(x+1)

So, input numbers and output numbers are

0 ==> 2, 2 ==> 6, 5 ==> 12

Example 5 :

Rule : Multiply the input number by itself then add one

Output numbers : {2, 5, 17}

Solution :

Let x and y be input and output respectively.

Multiply the input number by itself  =  x(x)

=  x²

add one  =  x² +1

Example 6 :

Rule : Multiply the input number by one more than itself.

Output numbers {2, 6, 20}

Solution :

Let x and y be input and output respectively.

According to given rule,

y  =  x(x+1)

y  =  x² + x

when y  =  2

2  =  x² + x

x² + x – 2  =  0

(x – 1) (x + 2)  =  0

x  =  1, -2

1 and -2 ==> 2

when y  =  6

6  =  x² + x

x² + x – 6  =  0

(x + 3) (x – 2)  =  0

x  =  2, -3

2 and -3 ==> 6

when y  =  20

20  =  x² + x

20  =  x² + x

x² + x – 20  =  0

(x + 5) (x – 4)  =  0

x  =  4, -5

4 and -5 ==> 20

So, input numbers and output numbers are

1 and -2 ==> 2, 2 and -3 ==> 6 and 4 and -5 ==> 20

Example 7 :

A farmer sells potatoes and tomatoes in a market. During the day, he gets 3 customers.

• The first customer demands 2 kg of potatoes and 1 kg of tomatoes.
• The second customer demands 1 kg of potatoes and 2 kg of tomatoes.
• The third customer demands 5 kg of potatoes and 2 kg of tomatoes.
• The price of potatoes per kg is $30 and the price of tomatoes per kg is $20.

a) Draw the input-output table for the given situation and find the revenue earned by the farmer from each customer and the total revenue.

b) Formulate a mathematical expression to show the relationship between the price of potatoes and tomatoes, the quantities sold and the revenue.

c) If a fourth customer visits his shop and demands 3 kg of potatoes and 2 kg of tomatoes, calculate the total revenue earned by the farmer using the mathematical equation formulated in question b.

a)  First customer :

Output = 30(2) + 20(1)

= 60 + 20

= $80

Second customer :

Output = 30(1) + 20(2)

= 30 + 40

= $70

Third customer :

Output = 30(5) + 20(2)

= 150 + 40

= $190

b) Total revenue = 80 + 70 + 190

= $340

c) Revenue of fourth customer :

Output = 30(3) + 20(2)

= 90 + 40

= $130

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.