FIND INVERSE FUNCTION FROM THE GIVEN FUNCTION

For each of the following functions :

Example 1 :

a) f(x)  =  2x+5     b) f(x)  =  (3-2x)/4     c) f(x)  =  x+3

(i) Find f^-1(x)

(ii) sketch y  =  f(x), y  =  f^-1(x) and y  =  x on the same axes.

Solution :

a) f(x)  =  2x+5

(i)

Step 1 :

Let, y  =  f(x)

y  =  2x+5

Step 2 :

By interchanging x and y, we get

x  =  2y+5

2y  =  x-5

y  =  (x-5)/2

Step 3 :

So, the required inverse function is

f^-1(x)  =  (x-5)/2

(ii)  By applying some random values of x in the function

y  =  2x+5

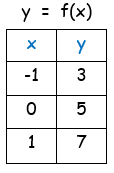By joining the points (-1, 3), (0, 5) and (1, 7), we will get the graph of original function. So, the required coordinates of inverse function are (3,-1) (5, 0) and (7, 1).

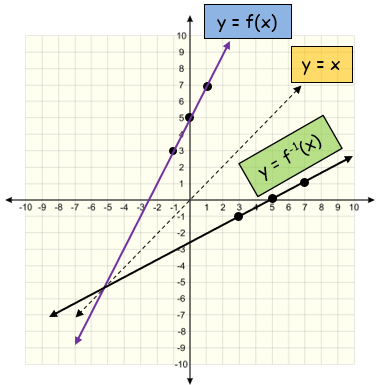
We draw the graph of inverse function be reflecting the graph of original function about y = x.

b)  f(x)  =  (3-2x)/4

Solution :

(i)  Let, y  =  f(x)

y  =  (3-2x)/4

By interchanging x and y, we get

x  =  (3-2y)/4

4x  =  3-2y

2y  =  3-4x

y  =  (3-4x)/2

y  =  -2x+(3/2)

We express f^-1 as a function of x in terms of y

f^-1(x)  =  -2x+(3/2)

(ii)  For graphing, by applying some random values of x in the function

 y  =  -2x+(3/2)

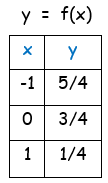By joining the points (-1, 5/4), (0, 3/4) and (1, 1/4), we will get the graph of original function. So, the required coordinates of inverse function are (5/4, -1), (3/4, 0) and (1/4, 1)

By plotting the points, we get graph of the given function and inverse function.

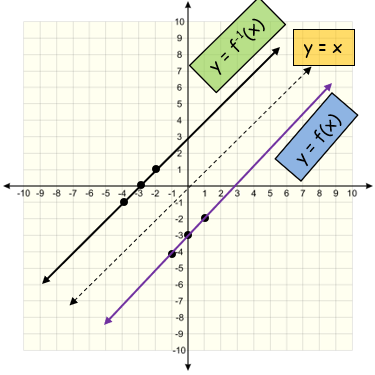
c) f(x)  =  x+3

Solution :

(i)  Let, y  =  f(x)

y  =  x+3

By interchanging x and y, we get

x  =  y+3

y  =  x-3

We express f^-1 as a function of x in terms of y

f^-1(x)  =  x-3

(ii) 

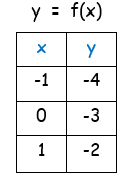Coordinates of given function : (-1, -4) (0, -3) and (1, -2) Coordinates of inverse function : (-4, -1) (-3, 0) and (-2, 1)

Example 2 :

If f(x)  =  2x + 7, find :

a) f^-1(x)        b) f(f^-1(x))        c) f^-1(f(x))

Solution :

a.

Given, f(x)  =  2x + 7

Let y  =  2x+7

By interchanging x and y, we get

x  =  2y+7

2y  =  x-7

y  =  (x-7)/2

We express f^-1 as a function of x in terms of y

f^-1(x)  =  (x-7)/2

b)

We have, f^-1(x)  =  (x-7)/2

Then,

f(f^-1(x))  =  f((x-7)/2)

=  2x+7

=  2[(x-7)/2] + 7

=  x–7+7

f(f^-1(x))  =  x   ----(1)

c)

we have, f^-1(x)  =  (x-7)/2

f^-1(f(x))  =  (f(x) - 7)/2

=  (2x+7-7)/2

=  2x/2

f^-1(f(x))  =  x ----(2)

Example 3 :

If f(x)  =  (2x + 1)/(x + 3), find :

a) f^-1(x)     b) f(f^-1(x))     c) f^-1(f(x))

Solution :

a) 

Given, f(x)  =  (2x+1)/(x+3)

Let y  =  (2x+1)/(x+3)

By interchanging x and y, we get

x  =  (2y+1)/(y+3)

x(y+3)  =  2y+1

xy+3x  =  2y+1

-2y+xy  =  -3x+1

y(-2+x)  =  -3x+1

y  =  (-3x+1)/(x-2)

y  =  (1-3x)/(x-2)

We express f^-1 as a function of x in terms of y

f^-1(x)  =  (1-3x)/(x-2)

b)  f(f^-1(x))  =  f((1-3x)/(x-2))

By using x in terms of f(x), we get

f(x)  =  (2x+1)/(x+3)

=  [2[(1-3x)/(x-2)]+1]/[(1-3x)/(x-2)+3]

=  [(2-6x+x-2)/(x-2)]/[(1-3x+3x-6)/(x-2)]

=  (-5x)/(-5)

=  x

f(f^-1(x))  =  x  ------(1)

c)  we have, f^-1(x)  =  (1-3x)/(x-2)

By using f(x) in terms of f^-1(x), we get

f^-1(f(x))  =  (1-3f(x))/(f(x)-2)

simplifying the terms,

=  [1-3(2x+1)/(x+3)]/[(2x+1)/(x+3)-2)

=  [(x+3) – 3(2x+1)/(x+3)]/[(2x+1) – 2(x+3)/(x+3)]

=  [x+3–6x–3]/[2x+1–2x–6]

=  (-5x)/(-5)

=  x

f^-1(f(x))  =  x  ------(2)

Example 4 :

You need a total of 50 pounds of two types of ground beef costing $1.25 and $1.60 per pound, respectively. A model for the total cost of the two types of beef is

y = 1.25x + 1.60(50 - x)

where is the number of pounds of the less expensive ground beef.

(a) Find the inverse function of the cost function. What does each variable represent in the inverse function?

(b) Determine the number of pounds of the less expensive ground beef purchased when the total cost is $73.

Solution :

a)  

y = 1.25x + 1.60(50 - x)

y = 1.25x + 80 - 1.60x

y = -0.35x + 80

Solving for x, we get

0.35x = 80 - y

x = (80 - y)/0.35

f^-1(x) = (80 - x)/0.35

b)  y = 1.25x + 1.60(50 - x)

y = 73

73 = 1.25x + 80 - 1.60x

73 = -0.35x + 80

73 - 80 = -0.35x

-7 = -0.35x

x = 7/0.35

x = 20

So, 20 pounds is the answer.

Example 5 :

The function given by

f(x) = k(2 - x - x²)

has an inverse function f^-1(3) = -2, find k.

Solution :

Domain of function f(x) is range of inverse function.

Instead of finding inverse of given function, we apply -2 in the original function f(x) to get the value of f^-1(3).

When input x = -2, output = 3

f(2) = k(2 - 2 - 2²)

3 = k(-4)

k = -3/4

So, the required value of k is -3/4.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.