FIND MINOR AND COFACTOR OF MATRIX

Minor of a matrix :

Let |A| = |[a ij]| be a determinant of order n.

The minor of an arbitrary element a_ij is the determinant obtained by deleting the i^th row and j^th column in which the element a_ij stands. The minor of a_ij by M_ij.

Cofactors :

The co factor is a signed minor. The cofactor of a_ij is denoted by A_ij and is defined as

A_ij  =  (-1)^(i+j) M_ij

Problem 1 :

Find the minor and cofactor of the following matrix.

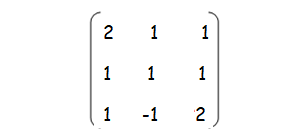
Solution :

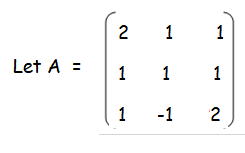
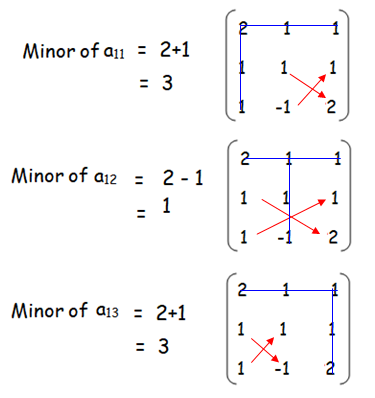
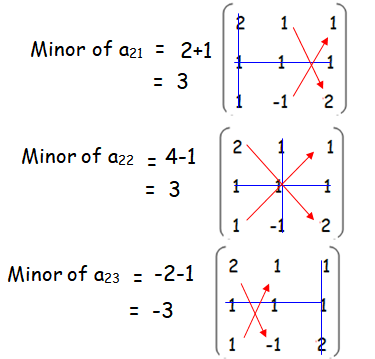
Problem 2 :

Find the minor and cofactor of the following matrix.

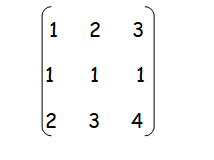
Solution :

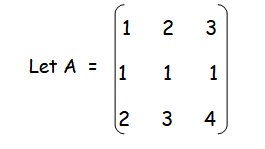
Minor of a₁₁  =  4-3  ==>  1

Minor of a₁₂  =  4-2  ==>  2

Minor of a₁₃  =  3-2  ==>  1

Minor of a₂₁  =  8-9  ==>  -1

Minor of a₂₂  =  4-6  ==>  -2

Minor of a₂₃  =  3-4  ==> -1

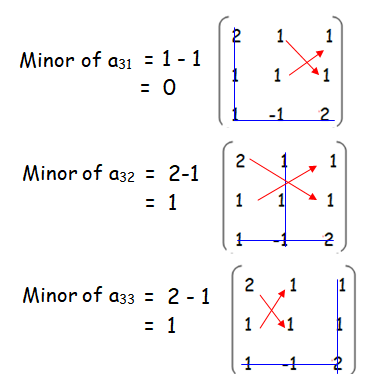
Minor of a₃₁  =  2-3  ==> -1

Minor of a₃₂  =  1-3  ==> -2

Minor of a₃₃  =  1-2  ==> -1

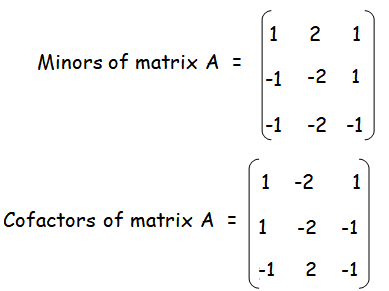
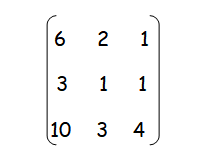
Problem 3 :

Find the minor and cofactor of the following matrix.

Solution :

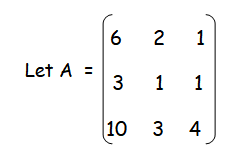
Minor of a₁₁  =  4-3  ==>  1

Minor of a₁₂  =  12-10  ==>  2

Minor of a₁₃  =  9-10  ==>  -1

Minor of a₂₁  =  8-3  ==>  5

Minor of a₂₂  =  24-10  ==>  14

Minor of a₂₃  =  18-20  ==> -2

Minor of a₃₁  =  2-1  ==> 1

Minor of a₃₂  =  6-3  ==> 3

Minor of a₃₃  =  6-6  ==> 0

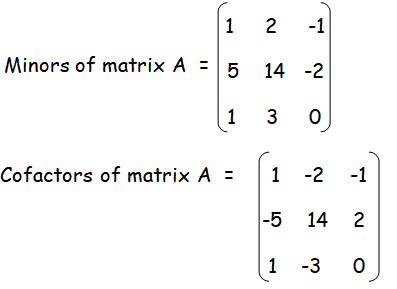
Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.