FIND MINOR OF MATRIX
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Minor of a matrix :
Let |A| = |[a ij]| be a determinant of order n.
The minor of an arbitrary element aij is the determinant obtained by deleting the ith row and jth column in which the element aij stands. The minor of aij by Mij.
Problem 1 :
Find the minor and cofactor of the following matrix.
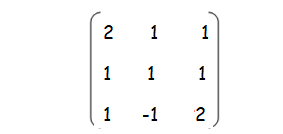
Solution :
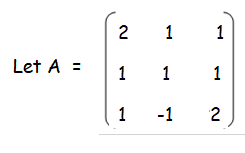
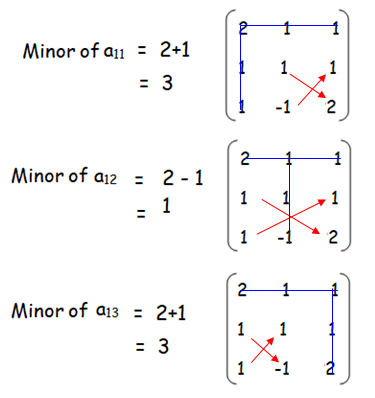
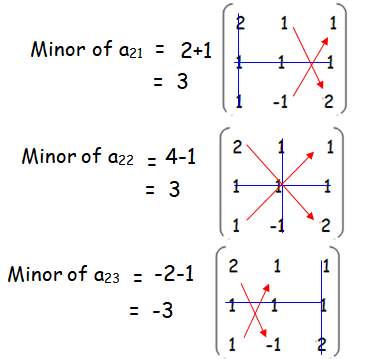
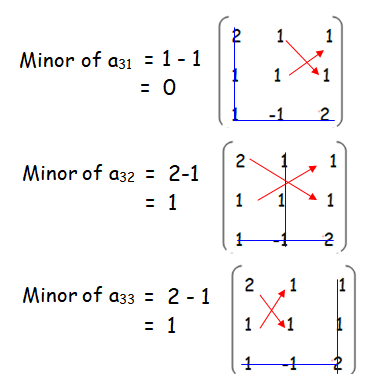
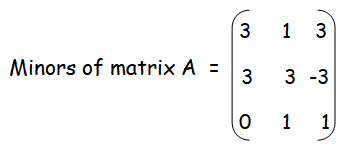
Problem 2 :
Find the minor and cofactor of the following matrix.
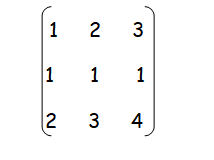
Solution :
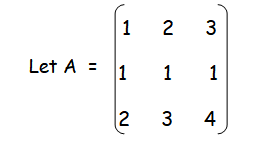
Minor of a11 = 4-3 ==> 1
Minor of a12 = 4-2 ==> 2
Minor of a13 = 3-2 ==> 1
Minor of a21 = 8-9 ==> -1
Minor of a22 = 4-6 ==> -2
Minor of a23 = 3-4 ==> -1
Minor of a31 = 2-3 ==> -1
Minor of a32 = 1-3 ==> -2
Minor of a33 = 1-2 ==> -1
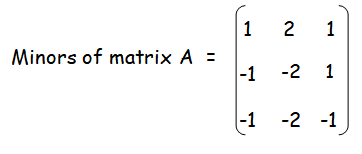
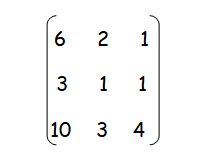
Problem 3 :
Find the minor and cofactor of the following matrix.
Solution :
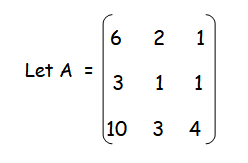
Minor of a11 = 4-3 ==> 1
Minor of a12 = 12-10 ==> 2
Minor of a13 = 9-10 ==> -1
Minor of a21 = 8-3 ==> 5
Minor of a22 = 24-10 ==> 14
Minor of a23 = 18-20 ==> -2
Minor of a31 = 2-1 ==> 1
Minor of a32 = 6-3 ==> 3
Minor of a33 = 6-6 ==> 0
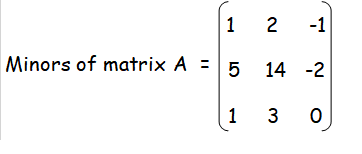
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact US | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 39)
Dec 11, 25 05:59 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation

