FIND MISSING VALUE FROM THE EQUATION OF PAIR OF STRAIGHT LINES
Example 1 :
Find p and q, if the following equation represents a pair of perpendicular lines
6x2 + 5xy − py2 + 7x + qy − 5 = 0
Solution :
If two lines are perpendicular, then a + b = 0
6x2 + 5xy − py2 + 7x + qy − 5 = 0
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
a = 6, b = -p
6 - p = 0
p = 6
If the given line represent the pair of straight line, then it must satisfy the condition given below.
abc + 2fgh - af2 - bg2 - ch2 = 0
a = 6, b = -6, 2h = 5 ==> h = 5/2, g = 7/2, f = q/2, c = -5
6(-6)(-5)+2(q/2)(7/2)(5/2)+6(q/2)2+6(7/2)2-(-5)(5/2)2=0
180 + (35q/4) - 6(q2/4) + 6(49/4) + 5(25/4) = 0
(720 + 35q - 6q2 + 294 + 125) / 4 = 0
1308 + 35q - 6q2 = 0
6q2 - 35q - 1139 = 0
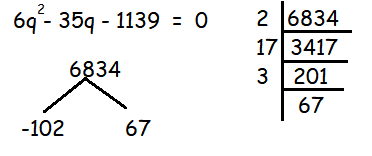
6q2 - 102q + 67q - 1139 = 0
6q (q - 17) + 67 (q - 17) = 0
(6q + 67) (q - 17) = 0
6q + 67 = 0 q - 17 = 0
q = -67/6 q = 17
Example 2 :
Find the value of k, if the following equation represents a pair of straight lines. Further, find whether these lines are parallel or intersecting, 12x2 + 7xy − 12y2 − x + 7y + k = 0
Solution :
To check the pair of straight lines is parallel or intersecting, we have to find the separate equation.
= 12x2 + 7xy − 12y2
= 12x2 + 16xy - 9xy − 12y2
= 4x(3x + 4y) - 3y(3x + 4y)
= (4x - 3y) (3x + 4y)
Separate equations are (4x - 3y + l) (3x + 4y + m)
12x2 + 7xy − 12y2 − x + 7y + k = (4x - 3y + l) (3x + 4y + m)
-1 = 4m + 3l ----(1)
7 = -3m + 4l ----(2)
(1) ⋅ 3 + (2) ⋅ 4 ==> 12m + 9l - 12m + 16l = -3 + 28
25l = 25 ==> l = 1
By applying the value of l in the first equation, we get
4m + 3(1) = -1
4m = -1 - 3
m = -1
(4x - 3y + 1) (3x + 4y - 1)
k = lm = 1(-1) = -1
Hence the value of k is -1
Example 3 :
For what value of k does the equation 12x2+2kxy+2y2+11x−5y+2 = 0 represent two straight lines.
Solution :
12x2+2kxy+2y2+11x−5y+2 = 0
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
a = 12, 2h = 2k ==> h = k, b = 2, g = 11/2, f = -5/2, c = 2
abc + 2fgh - af2 - bg2 - ch2 = 0
12(2)(2) + 2(-5/2)(11/2)k - 12(-5/2)2 - 2(11/2)2 - 2k2 = 0
48 + (-55k/2) - 75 - (121/2) - 2k2 = 0
96 - 55k - 150 - 121 - 4k2 = 0
4k2+ 55k + 175 = 0
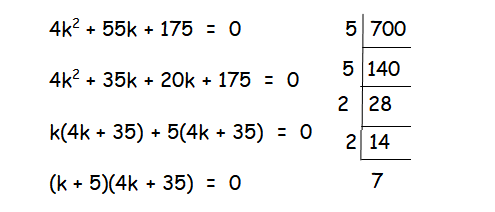
|
k + 5 = 0 k = -5 |
4k + 35 = 0 k = -35/4 |
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 8)
Jan 30, 25 09:48 AM
AP Calculus AB Problems with Solutions (Part - 8) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 29, 25 06:00 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 105)
Jan 29, 25 05:52 AM
Digital SAT Math Problems and Solutions (Part - 105)
