FIND SLOPE X INTERCEPT AND Y INTERCEPT OF THE LINE

Find

(a)  gradient

(b)  x-intercept and

(c)  y-intercept

for the equation of line.

Example 1 :

2x–3y  =  6

Solution :

2x-3y  =  6

m  =  -coefficient of x/coefficient of y

m  =  -2/(-3)

m  =  2/3

So, the required slope, x and y intercepts are 2/3, 3 and -2 respectively.

Example 2 :

4x+5y  =  20

Solution :

4x+5y  =  20

m  =  -coefficient of x/coefficient of y

m  =  -4/5

Example 3 :

y  =  - 2x + 5

Solution :

The given equation is in slope intercept form. 

We compare y  =  - 2x + 5 and y  =  mx + b we get,

m  =  - 2 and b  =  5

Then we find the x-intercept form,

Let y  =  0

By applying y  =  0 in given equation, we get

y  =  - 2x + 5

0  =  - 2x + 5

2x  =  5

x  =  5/2

Example 4 :

x  =  8

Solution :

Standard form of linear equation.

ax+by+c  =  0

x-8  =  0

x+0y-8  =  0

m = -coefficient of x/coefficient of y

m  =  1/0

Slope(m)  =  undefined

x-intercept  =  8

y-intercept  =  0

Example 5 :

y  =  5

Solution :

Standard form of linear equation.

ax+by+c  =  0

y-5  =  0

0x+y-5  =  0

m = -coefficient of x/coefficient of y

m  =  0/1

m  =  0

x-intercept  =  0

y-intercept  =  5

Example 6 :

x + y  =  11

Solution :

x+y  =  11

m  =  -coefficient of x/coefficient of y

m  =  -1/1

m  =  -1

Example 7 :

A balloon is released from the top of a building. The graph shows the height of the balloon over time

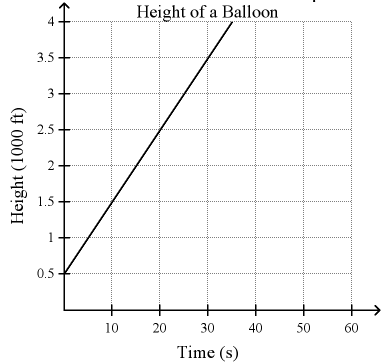
a) What does the slope and y-intercept reveal about the situation?

b) For a similar situation, the slope 35 is and the y-intercept is 550. What can you conclude?

Solution :

a)  Slope of the line shown :

(0, 0.5) and (10, 1.5)

Slope (m) = (y₂ - y₁) / (x₂ - x₁)

= (1.5 - 0.5) / (10 - 0)

= 1/10

Rise = 1 and run = 10

Equation of line :

y - y₁ = m(x - x₁)

y - 0.5 = 0.1(x - 0)

y - 0.5 = 0.1x

y = 0.1x + 0.5

Slope = 0.1 and y-intercept = 0.5

Initial height = 0.5

For every 10 seconds 1 ft height is increasing.

b)  The balloon starts at a height of 500, and rises at a rate of 100; The balloon starts at a height of 550, and rises at a rate of 35.

Example 8 :

A line has a slope of 6 and an x-intercept of 7.

a. Write the equation for the line in slope-intercept form. Justify your work.

b. Another line, with the same slope as the first, passes through the point (–1, –1).

Find the equation of this line

Solution :

a)  slope of 6 and an x-intercept of 7

y = mx + b

y = 6x + 7

b) Slope is the same, then slope of the new line m = 6 and passes through the point (-1, -1).

y - y₁ = m(x - x₁)

y - (-1) = 6(x - (-1))

y + 1 = 6(x + 1)

y = 6x + 6 - 1

y = 6x + 5

Example 9 :

Mary was told that a line goes through the points (1, 3) and (6, –2) and has a slope of 3.

a. Explain why the information Mary was given cannot be correct.

b. If the given point (1, 3) and the given slope are correct, what is the equation for the line?.

Solution :

a) Slope of the line passes through points (1, 3) and (6, -2)

Slope (m) = (y₂ - y₁) / (x₂ - x₁)

= (-2 - 3) / (6 - 1)

= -5/5

= -1

Using the formula, we get the slope -1. But the given slope is 3

b) Slope m = -1

(1, 3)

Equation of the line has slope and given point.

y - y₁ = m(x - x₁)

y - 3 = -1(x - 1)

y = -x + 1 + 3

y = -x + 4

So, the required equation is y = -x + 4.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.