FIND THE AREA OF THE SHADED REGION USING POLYNOMIALS

Find the shaded area A in terms of x for :

Example 1 :

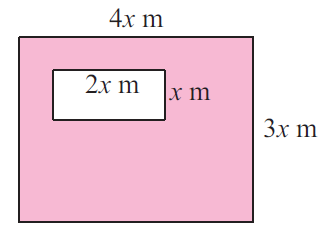
Solution :

Area of shaded region 

=  Area of large rectangle - Area of small rectangle

Area of rectangle  =  length ⋅ width

Large rectangle :

Length  =  4x and width  =  3x

Area of large rectangle  =  (4x ⋅ 3x) 

=  12x²

Small rectangle :

Length  =  2x and width  =  x

Area of small rectangle  =  (2x ⋅ x)

=  2x²   -------(2)

(1) - (2)

=  12x²-2x²

=  10x²

So, area of shaded region is 10x² square meter.

Example 2 :

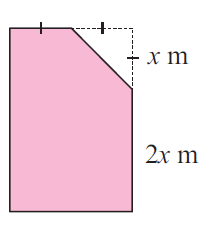
Solution :

Shaded region 

=  Area of rectangle - Area of triangle

Area of rectangle  =  length ⋅ width and 

Area of triangle  =  (1/2) ⋅ base ⋅ height

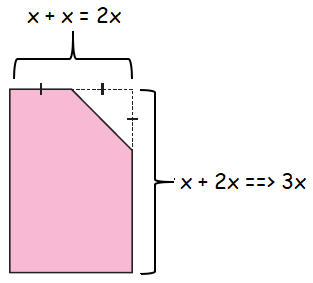
Length  =  3x and width  =  2x

Area of rectangle  =  3x(2x)  ==>  6x² ---(1)

Area of triangle  =  (1/2)⋅ x ⋅ x

=  x²/2 ---(2)

(1) - (2)

Area of shaded region  =  6x² - (x²/2)

=  (12x² - x²)/2

=  11x²/2

So, area of shaded region is 11x²/2 square meter.

Example 3 :

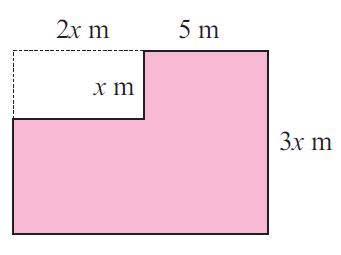
Solution :

Area of shaded region 

=  Area of large rectangle - Area of small rectangle

Large rectangle :

length  =  2x+5, width  =  3x

Area of large rectangle  =   3x(2x+5) 

=  6x² + 15x  ----(1)

Small rectangle :

length  =  2x, width  =  x

Area of small rectangle  =  2x(x)

=  2x²  ----(2)

(1) - (2)

Area of shaded region  =  6x² + 15x - 2x²

Combining like terms, we get

=  4x² + 15x

So, area of shaded region is 4x² + 15x square meter.

Example 4 :

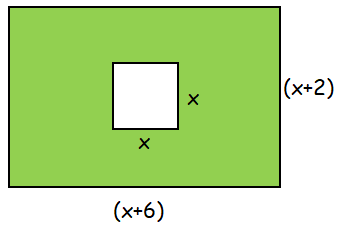
Solution :

Area of shaded region 

=  Area of rectangle - Area of square

Rectangle :

Length  =  x+6, width  =  x+2

Area of rectangle  = (x+6)(x+2)

=  x²+2x+6x+12

=  x²+8x+12  ----(1)

Square :

Side length  =  x

Area of square  =  x² ----(2)

(1) - (2)

Area of shaded region  =  x²+8x+12-x²

By combining like term, we get

=  8x+12

So, area of shaded region is 8x+12 square meter.

Example 5 :

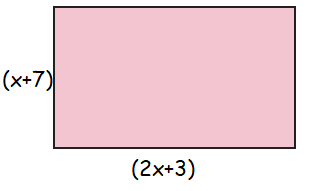
Solution :

Area of rectangle  =  length ⋅ width

=  (2x+3)(x+7)

=  2x(x) + 2x(7) + 3(x) + 3(7)

=  2x² + 14x + 3x + 21

=  2x² + 17x+ 21

So, area of rectangle is 2x² + 17x+ 21 square meter. 

Example 6 :

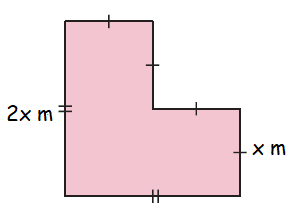
Solution :

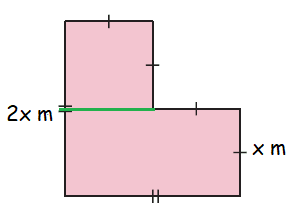
Area of shaded region 

=  Area of rectangle + Area of square

Rectangle :

Length  =  2x and width  =  x 

Area of rectangle  =  2x(x)

=  2x²

Square :

Length of square  =  x

Area of square  =  x(x)

=  x²

Area of shaded region  =  2x² + x²

=  3x²

So, area of shaded region is 3x² square meter.

Example 7 :

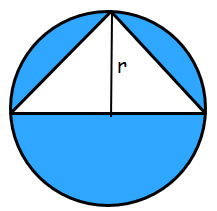
Solution :

Area of shaded region  =  Area of circle - Area of triangle

Area of circle  =  πr²

Area of triangle  =  (1/2) ⋅ (2r) ⋅ r  ==>  r²

Area of shaded region  =  πr² - r²

=  r²(π - 1)

So, area of shaded region is r²(π - 1) square meter.

Example 8 :

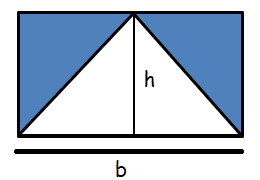
Solution :

Area of shaded region  =  Area of rectangle - Area of triangle

Area of circle  =  bh

Area of triangle  =  (1/2) ⋅ b ⋅ h  ==>  bh/2

Area of shaded region  =  bh - (bh/2)

=  (bh/2)

So, area of shaded region is (bh/2) square meter.

Example 9 :

Find the area of the shaded region.

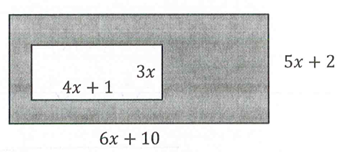
Solution :

Area of shaded region = (6x + 10)(5x + 2) - 3x(4x + 1)

= 30x² + 12x + 50x + 12 - 12x² - 3x

= 30x² - 12x² + 12x + 50x - 3x + 12  

= 18x² + 59x + 12

Example 10 :

Kyle creates a canvas painting on a rectangular canvas with that is four inches longer than the height.

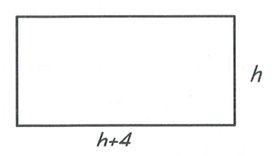
a) Write the polynomial expression, in simplified form that represents the area of the canvas.

b) Kyle adds 3 inch wide frame around all sides of his canvas. Write the polynomial expression, in simplified form that represents the total area of the frame.

Solution :

i)

Area of canvas = area of rectangle

Length of rectangle = h + 4

width of the rectangle = h

Area = h(h + 4)

= h² + 4h

ii)  After extending 3 inches by the side, we get

Length = h + 4 + 3 + 3 ==> h + 10

Width = h + 3 + 3 ==> h + 6

Total area of the frame = (h + 10)(h + 6)

= h² + 10h + 6h + 60

= h² + 16h + 60

Example 11 :

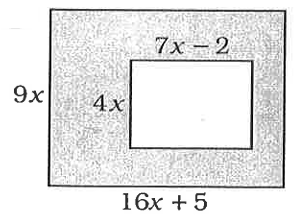
Solution :

Area of the shaded region

= Area of the large rectangle - area of the small rectangle

= 9x(16x + 5) - 4x(7x - 2)

= 144x² + 45x - 28x² + 8x

Combining the like terms, we get

= 116x² + 53x

Example 12 :

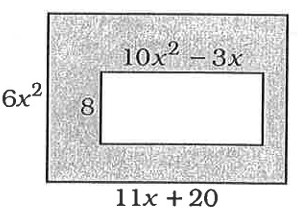
Solution :

Area of the shaded region

= Area of the large rectangle - area of the small rectangle

= 6x²(11x + 20) - 8(10x² - 3x)

= 66x³ + 120x² - 80x² + 24x

= 66x³ + 40x² + 24x

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.