FIND THE AREA OF OF THE SHADED REGION WITH POLYNOMIALS

Find the area A of the shaded regions if all sides are given in m:

Example 1 :

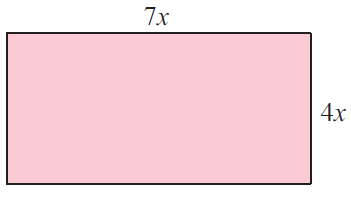
Solution :

Area of shaded region  =  Area of rectangle

length  =  7x and width  =  4x

Area of rectangle  =  7x(4x)

=  28x²

So, area of shaded region is 28x² square meter.

Example 2 :

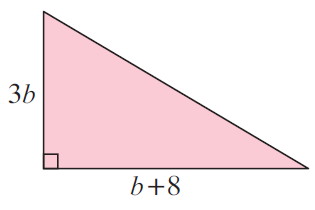
Solution :

Area of triangle  =  (1/2) ⋅ base ⋅ height

Base  =  b+8 and height  =  3b

=  (1/2) ⋅ (b+8) ⋅ 3b

=  (1/2) (3b²+24b) 

=  3b²/2+24b/2 

=  3b²/2+12b

Example 3 :

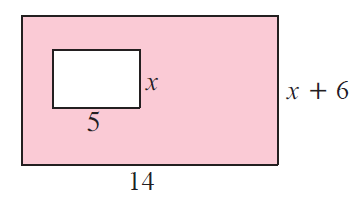
Solution :

Area of shaded region 

=  Area of large rectangle - Area of small rectangle

Large rectangle :

length  =  14, width  =  x + 6

Area of large rectangle  =  14(x+6)

=  14x + 84  ---(1)

Small rectangle :

length  =  5, width  =  x

Area of large rectangle  =  5(x)  ==>  5x  ---(2)

(1) - (2)

Area of shaded region  =  14x + 84 - 5x

=  9x+84 

So, area of shaded region is (9x+84) square meter.

Example 4 :

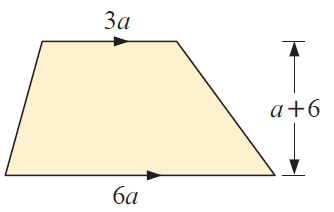
Solution :

Area of trapezium  =  (1/2) ⋅ h ⋅ (a+b)

h = height and a, b are parallel sides.

h  =  a+6, a  =  6a and b  =  3a

Area of trapezium  =  (1/2) ⋅ (a+6) ⋅ (6a+3a)

=  (1/2) ⋅ (a+6) ⋅ (9a)

=  (1/2) ⋅ (9a²+54a)

=  (9a²/2) + (54a/2)

=  (9a²/2) + 27a

So, the area of shaded region is (9a²/2) + 27a square meter.

Example 5 :

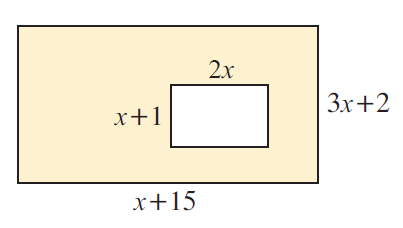
Solution :

Area of shaded region 

=  Area of large rectangle - Area of small rectangle

Larger rectangle :

length  =  x + 15 and width  =  3x + 2

Area of large rectangle  =  (x+15) (3x+2)

=  3x²+2x+45x+30

=  3x²+47x+30  ------(1)

Small rectangle :

Length  =  2x and width  =  x + 1

Area of large rectangle  =  (2x) (x+1)

=  2x²+2x ------(2)

(1) - (2)

Area of shaded region  =  3x²+47x+30 - (2x²+2x)

=  3x²-2x²+47x-2x+30

=  x²+45x+30

So, area of shaded region is (x²+45x+30) square meter.

Example 6 :

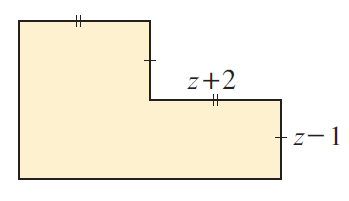
Solution :

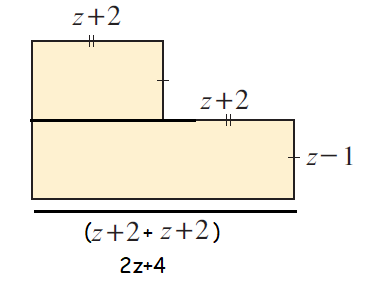
Area of shaded region 

=  Area of large rectangle + Area of small rectangle

Large rectangle :

Length = 2z+4, width  = z-1

Area of large rectangle  =  (2z+4)(z-1)

=  2z²-2z+4z-4

=  2z²+2z-4  ------(1)

Small rectangle :

Length = z+2, width  = z-1

Area of small rectangle  =  (z+2)(z-1)

=  z²-z+2z-2

=  z²+z-2 ------(2)

(1) + (2)

Area of shaded region =  2z²+2z-4 + z²+z-2

Combining like terms, we get

=  3z²+3z-6

So, area of shaded region is 3z²+3z-6 square meter.

Example 7 :

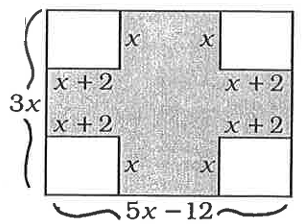
Solution :

Area of the shaded region

= Area of large rectangle - 4(area of small rectangles at the corner

= 3x(5x - 12) - 4x(x + 2)

= 15x² - 36x - 4x² - 8x

Combining the like terms, we get

= 11x² - 44x

Example 8 :

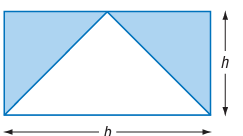
Solution :

Area of shaded region

= Area of rectangle - area of triangle

= length x width - (1/2) base x height

= h (h) - (1/2) x (h) (h)

= h² - (1/2)h²

= (2h² - 1h²)/2

= h²/2

So, area of the shaded portion is h²/2 square units.

Example 9 :

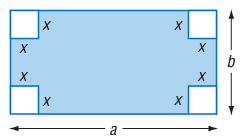
Solution :

Area of shaded region

= Area of rectangle - 4(area of square)

Measures of large rectangle :

length = a, width = b

Measures of small square :

side length = x

Area of shaded region = ab - 4x²

Example 10 :

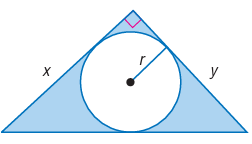
Solution :

Area of shaded region = Area of triangle - area of circle

= (1/2) x base x height - πr²

= (1/2) xy - πr²

Example 11 :

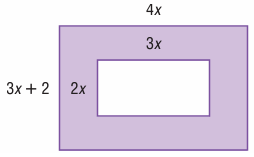
Solution :

Area of shaded portion = area of large rectangle - area of small rectangle

= 4x (3x + 2) - 2x(3x)

= 12x² + 8x - 6x²

Combining the like terms, we get

= 6x² + 8x

Example 12 :

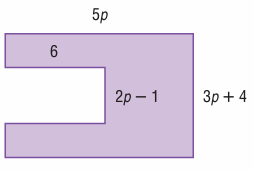
Solution :

Area of shaded portion

= area of large rectangle - area of small rectangle

= 5p(3p + 4) - 6(2p - 1)

= 15p² + 20p - 12p + 6

= 15p² + 8p + 6

Example 13 :

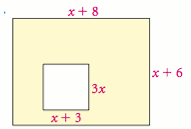
Solution :

Area of shaded portion = Area of large rectangle - area of small rectangle

= (x + 8)(x + 6) - 3x(x + 3)

= x² + 6x + 8x + 48 - 3x² - 9x

Combining the like terms, we get

= x²  - 3x² + 48  - 9x + 6x + 8x

= -2x² + 5x + 48

Example 14 :

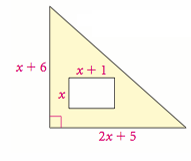
Solution :

Area of shaded portion = Area of triangle - area of rectangle

= (1/2) (x + 6)(2x + 5) - x(x + 1)

= (1/2)(2 x² + 5x + 12x + 30) - x² - x

= (1/2)(2 x² + 17x + 30) - x² - x

= x² + (17/2)x + 15 - x² - x

= (17/2)x - x + 15 

= (15/2)x + 15

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.