FIND THE DISTANCE FROM A POINT TO THE LINE
The distance from the point to the line is the distance from the point to the foot of the perpendicular.
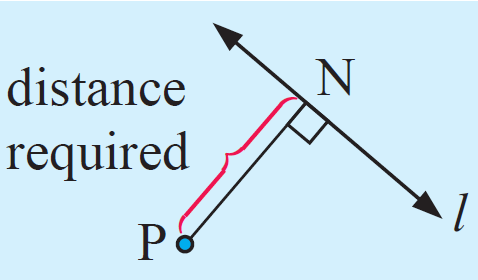
To find out the foot of perpendicular(N) drawn from the point P, we follow the steps given below.
Step 1 :
Since the lines are perpendicular, the product of their slopes will be equal to -1.
Step 2 :
Slope of perpendicular line = -1/Slope of given line
Step 3 :
Find the equation using the given point and slope what we have derived from step 2.
Step 4 :
Solve the system of equations to find point of intersection.
Step 5 :
Find the distance between two points.
Distance formula = √(x2–x1)2 + (y2–y1)2
Find the distance from :
Example 1 :
(7, - 4) to y = 3x - 5
Solution :
Step 1 :
y = 3x–5 -----(1)
By comparing the given equation with slope intercept form (y = mx+b).
slope (m) = 3
Step 2 :
Slope of perpendicular line = -1/3
Step 3 :
Find the equation of the perpendicular line passes through (7, -4).
(7, -4) ----->(x1, y1)
m = -1/3
(y–y1) = m(x–x1)
(y+4) = - 1/3(x–7)
3(y+4) = -1(x-7)
3y = -x+7-12
3y = -x-5 ---(2)
Step 4 :
Find the point of intersection of two lines,
By applying (1) in (2), we get
|
3(3x–5) = -x-5 9x-15 = -x-5 x = 1 |
3y = -1-5 3y = -6 y = -2 |
Foot of perpendicular is (1, -2).
Step 5 :
Distance between two points :
= √(1–7)2 + (-2+4)2
= √40
= 2√10 units.
So, the required distance is 2√10 units.
Example 2 :
(-6, 0) to y = 3–2x
Solution :
y = 3–2x ----(1)
By comparing the given equation with y = mx+b, we come so know slope (m)
Slope (m) = - 2
Slope of perpendicular line = 1/2
Equation of perpendicular line :
(y - 0) = 1/2(x + 6)
2y = x+6 ----(2)
Applying (1) in (2), we get
|
2(3–2x) = x+6 6-4x = x+6 -5x = 0 x = 0 |
2y = 0+6 2y = 6 y = 3 |
So, foot of perpendicular is (0, 3).
Distance between (-6, 0) and (0, 3).
= √(0+6)2 + (3-0)2
= √(36+9)
= √45
= 3√5 units.
So, the required distance is 3√5 units.
Example 3 :
Shown on the grid is the line, y = x +1
(a) Find the gradient of a line perpendicular to y = x + 1
(b) Find the equation of the line perpendicular to y = x + 1 that passes through the point (5, 0)
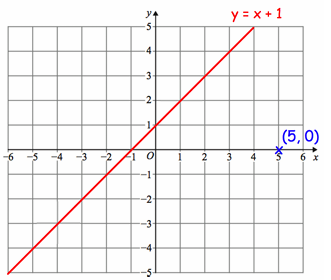
(c) Find the point where your answer to (b) and the line y = x + 1 intersect.
(d) Calculate the distance between your answer to (c) and the point (5, 0)
Solution :
(a) Slope of the line y = x + 1
Comparing with y = mx + b, we know that m = 1.
(b) Slope of the line y = x + 1 is 1. since the required line is perpendicular to the required line, we have to use -1/m to find the slope of the perpendicular line.
-1 is the slope and passes through the point (5, 0).
y - 0 = -1(x - 5)
y = -x + 5
c) Finding point of intersection of the line y = x + 1 and y = -x + 5.
x + 1 = -x + 5
x + x = 5 - 1
2x = 4
x = 2
Applying x = 2 in y = x + 1, we get y = 3
So, the required point of intersection is (2, 3).
d) Distance between the point (2, 3) and (5, 0).
= √(5 - 2)2 + (3 - 0)2
= √32 + 32
= √(9 + 9)
= √18
= √(2 x 3 x 3)
= 3√2 units.
So, the required distance is 3√2 units.
Example 4 :
- The line L1 has equation y = 2x - 4
- The line L2 has equation y = -3x + 11
- The line L3 has equation y = x
- L1 and L2 meet at the point A.
- Line 1 and line 3 are intersecting at B.
Work out the shortest distance between the points A and B.
Solution :
Let us find the point of intersection of L1 and L2.
y = 2x - 4 ------(1)
y = -3x + 11 -----(2)
(1) = (2)
2x - 4 = -3x + 11
2x + 3x = 11 + 4
5x = 15
x = 15/5
x = 3
Applying x = 3 in (1), we get
y = 2(3) - 4
y = 6 - 4
y = 2
So, the point of intersection of line 1 and line is A (3, 2).
y = 2x - 4 -----(3)
y = x -----(4)
x = 2x - 4
x - 2x = -4
-x = -4
x = 4
Applying x = 4 in (4)
y = 4
So, point B is (4, 4).
AB = √(4 - 3)2 + (4 - 2)2
= √12 + 22
= √(1+4)
= √5 units.
Calculate the shortest distance between the point G(-4, 4) and the line y = 3x- 4.
Solution :
Step 1 :
Determine the equation of the line passing through (-4, 4) and perpendicular to y = 3x- 4.
Slope of the given line y = 3x - 4 is 3
Slope of the perpendicular line :
-1/m = -1/3
Equation of the perpendicular line is
y - y1 = -1/m(x - x1)
y - 4 = -1/3(x + 4)
y = (-1/3) x - (4/3) + 4
y = (-1/3) x + (8/3)
Step 2 :
Solving y = 3x - 4 and y = (-1/3) x + (8/3)
3x - 4 = (-1/3) x + (8/3)
3x + x/3 = 8/3 + 4
10x / 3 = 20/3
10x = 20
x = 2
Applying x = 2, we get
y = 3(2) - 4
y = 2
So, (2, 2) is the required point. The distance between (-4, 4) and (2, 2).
Step 3 :
= √(-4 - 2)2 + (4 - 2)2
= √(-6)2 + (2)2
= √(36 + 4)
= √40
= 2√10 units
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 8)
Jan 30, 25 09:48 AM
AP Calculus AB Problems with Solutions (Part - 8) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 29, 25 06:00 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 105)
Jan 29, 25 05:52 AM
Digital SAT Math Problems and Solutions (Part - 105)
